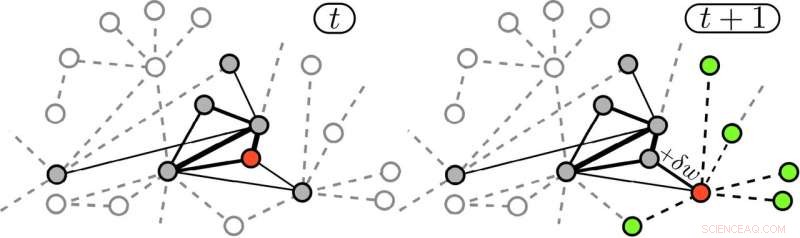
Las caminatas aleatorias reforzadas por los bordes producen una coevolución de la red con la dinámica de los caminantes. En el momento t, el caminante está en el nodo rojo y ya ha visitado los nodos grises, mientras que los nodos sombreados aún están inexplorados. Los anchos de los bordes son proporcionales a sus pesos. En el tiempo t + 1, el caminante se ha movido a un nodo vecino (rojo), y el peso del borde usado se ha reforzado con δw. En este punto, el caminante preferentemente regresará, aunque también puede acceder al conjunto de 'adyacentes posibles' (verde). Crédito:Iacopo Iacopini
Investigadores de la Universidad Queen Mary de Londres han desarrollado un modelo matemático para la aparición de innovaciones.
El estudio de los procesos creativos y la comprensión de cómo surgen las innovaciones y cómo las novedades pueden desencadenar nuevos descubrimientos podría conducir a intervenciones efectivas para fomentar el éxito y el crecimiento sostenible de la sociedad.
Los hallazgos empíricos han demostrado que la forma en que se descubren las novedades sigue patrones similares en una variedad de contextos diferentes, incluida la ciencia, letras, y Tecnología.
El estudio, publicado en Cartas de revisión física , introduce un nuevo marco matemático que reproduce correctamente la velocidad a la que surgen novedades en los sistemas reales, conocida como ley de Heaps, y puede explicar por qué los descubrimientos están fuertemente correlacionados y, a menudo, vienen en grupos.
Lo hace traduciendo la teoría de lo 'posible adyacente', formulado inicialmente por Stuart Kauffman en el contexto de los sistemas biológicos, en el lenguaje de redes complejas. Lo posible adyacente es el conjunto de todas las oportunidades novedosas que se abren cuando se realiza un nuevo descubrimiento. Las redes han surgido como una forma poderosa de investigar sistemas del mundo real, capturando las relaciones esenciales entre los componentes, y modelar la estructura oculta detrás de muchos fenómenos sociales complejos.
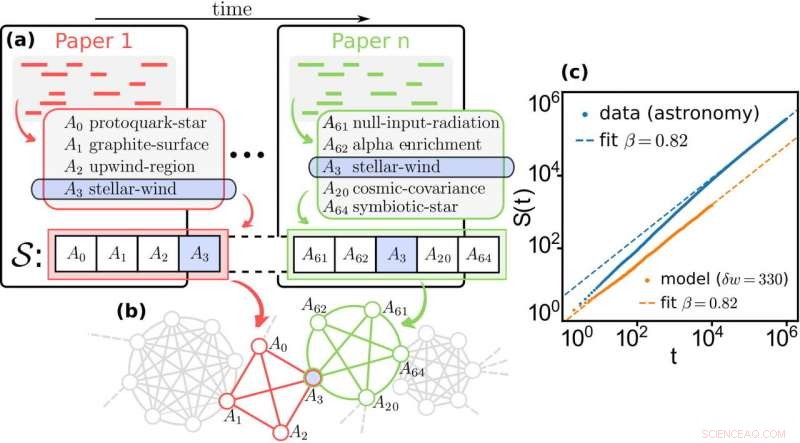
Crecimiento del conocimiento en ciencia. (a) Una secuencia empírica de conceptos científicos S se extrae de una secuencia temporalmente ordenada de artículos concatenando, para cada campo científico, los conceptos relevantes presentes en los resúmenes. (b) La red de relaciones entre conceptos se construye vinculando todos los conceptos que aparecen en el mismo resumen. Luego, la red se utiliza como estructura subyacente para ejecutar nuestro modelo de paseo aleatorio reforzado con bordes. (c) A continuación, el modelo se ajusta a los datos empíricos seleccionando la cantidad de refuerzo δw que reproduce el exponente β de Heaps obtenido al ajustar la curva de Heaps extraída de S como una ley de potencia. Crédito:Iacopo Iacopini
En este trabajo, Las redes se utilizan para modelar el espacio subyacente de relaciones entre conceptos.
El autor principal, el profesor Vito Latora, de la Escuela de Ciencias Matemáticas Queen Mary, dijo:"Esta investigación abre nuevas direcciones para el modelado de la innovación, junto con un nuevo marco que podría llegar a ser importante en la investigación de tecnologías, biológico, artístico, y sistemas comerciales ".
Añadió:"Estudiar los procesos a través de los cuales surgen las innovaciones puede ayudar a comprender los ingredientes principales detrás de una idea ganadora, una tecnología de vanguardia o una actividad comercial exitosa, y es fundamental para diseñar decisiones efectivas basadas en datos, estrategias, e intervenciones para fomentar el éxito y el crecimiento sostenible de nuestra sociedad ".
En el estudio, el proceso de descubrimiento se modela como una clase particular de paseos aleatorios, llamados paseos 'reforzados', sobre una red subyacente de relaciones entre conceptos e ideas. Una innovación corresponde a la primera visita de un sitio de la red, y cada vez que un caminante pasa de un concepto a otro, dicha asociación (un borde en la red) se refuerza para que se utilice con mayor frecuencia en el futuro. Los investigadores llamaron a esto el modelo de "caminata aleatoria reforzada con bordes".
Para mostrar cómo funciona el modelo en un caso real, también construyeron un conjunto de datos de 20 años de publicaciones científicas en diferentes disciplinas, como la astronomía, ecología, economía y matemáticas para analizar la aparición de nuevos conceptos. Esto demostró que, a pesar de su sencillez, el modelo de paseo aleatorio reforzado por bordes es capaz de reproducir cómo crece el conocimiento en la ciencia moderna.
El profesor Vito Latora agregó:"El marco que presentamos constituye un nuevo enfoque para el estudio de los procesos de descubrimiento, en particular aquellos para los que la red subyacente se puede reconstruir directamente a partir de datos empíricos, por ejemplo, los usuarios que escuchan música a través de una red de similitud entre canciones. Ya estamos trabajando en esta idea, junto con una versión ampliada de nuestro modelo, donde estudiamos la exploración colectiva de estos espacios en red considerando múltiples caminantes al mismo tiempo ".