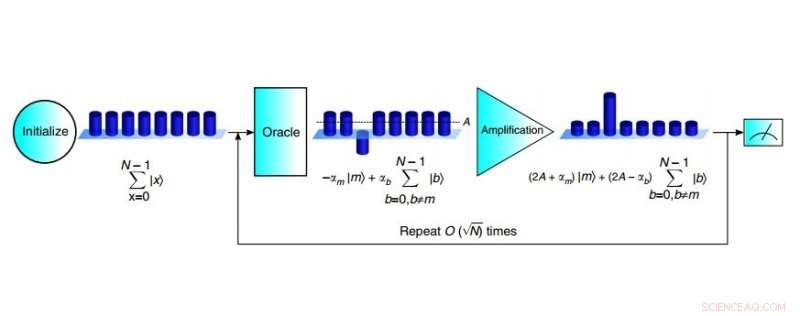
Las tres etapas del algoritmo de búsqueda Grover de 3 qubit:inicialización, oráculo, y amplificación. Crédito:C. Figgatt et al. Publicado en Comunicaciones de la naturaleza
Buscando grande, bases de datos desordenadas para un elemento deseado es una tarea que requiere mucho tiempo para las computadoras clásicas, pero se espera que las computadoras cuánticas realicen estas búsquedas mucho más rápidamente. Investigaciones anteriores han demostrado que el algoritmo de búsqueda de Grover, propuesto en 1996, es un algoritmo de búsqueda cuántica óptimo, lo que significa que ningún otro algoritmo cuántico puede buscar más rápido. Sin embargo, implementar el algoritmo de Grover en un sistema cuántico ha sido un desafío.
Ahora en un nuevo estudio, Los investigadores han implementado el algoritmo de Grover con iones atómicos atrapados. El algoritmo usa tres qubits, que corresponde a una base de datos de 8 (2 3 ) elementos. Cuando se utiliza para buscar en la base de datos uno o dos elementos, Las probabilidades de éxito del algoritmo de Grover fueron, como se esperaba, significativamente más altas que las mejores probabilidades de éxito teóricas para las computadoras clásicas.
Los investigadores, Caroline Figgatt y col., en la Universidad de Maryland y la Fundación Nacional de Ciencias, han publicado un artículo sobre sus resultados en un número reciente de Comunicaciones de la naturaleza .
"Este trabajo es la primera implementación de un algoritmo de búsqueda Grover de 3 qubit en un sistema de computación cuántica escalable, "Dijo Figgatt Phys.org . "Adicionalmente, esta es la primera implementación del algoritmo usando oráculos booleanos, que se puede comparar directamente con una búsqueda clásica ".
El enfoque clásico para buscar en una base de datos es sencillo. Básicamente, el algoritmo adivina aleatoriamente un elemento, o "solución". Entonces, por ejemplo, para una sola iteración de búsqueda en una base de datos de 8 elementos, un algoritmo clásico realiza una consulta aleatoria y, si eso falla, hace una segunda conjetura aleatoria; en total, adivinar 2 de 8 elementos, resultando en una tasa de éxito del 25%.
Algoritmo de Grover, por otra parte, primero inicializa el sistema en una superposición cuántica de los 8 estados, y luego usa una función cuántica llamada oráculo para marcar la solución correcta. Como resultado de estas estrategias cuánticas, para una sola iteración de búsqueda en una base de datos de 8 elementos, la tasa de éxito teórica aumenta al 78%. Con una tasa de éxito más alta, se obtienen tiempos de búsqueda más rápidos, ya que se necesitan menos consultas en promedio para llegar a la respuesta correcta.
En la implementación del algoritmo de Grover reportado aquí, la tasa de éxito fue menor que el valor teórico, aproximadamente 39% o 44%, dependiendo del oráculo utilizado, pero aún notablemente más alto que la tasa de éxito clásica.
Los investigadores también probaron el algoritmo de Grover en bases de datos que tienen dos soluciones correctas, en cuyo caso las tasas de éxito teóricas son 47% y 100% para computadoras clásicas y cuánticas, respectivamente. La implementación demostrada aquí logró tasas de éxito del 68% y el 75% para los dos tipos de oráculo; nuevamente, mejor que el valor teórico más alto para las computadoras clásicas.
Los investigadores esperan que, en el futuro, esta implementación del algoritmo de Grover se puede escalar a bases de datos más grandes. A medida que aumenta el tamaño de la base de datos, la ventaja cuántica sobre las computadoras clásicas crece aún más, que es donde se beneficiarán las aplicaciones futuras.
"Avanzando, planeamos continuar desarrollando sistemas con un control mejorado sobre más qubits, "Dijo Figgatt.
© 2018 Phys.org