
Una nueva técnica para hacer crecer cualquier forma objetivo a partir de cualquier forma inicial se demuestra al "hacer crecer" el rostro del padre de la física cuántica, Max Planck, de un disco plano. Crédito:Harvard SEAS
La naturaleza tiene una forma de hacer formas complejas a partir de un conjunto de reglas de crecimiento simples. La curva de un pétalo el golpe de una rama, incluso los contornos de nuestro rostro están moldeados por estos procesos. ¿Qué pasaría si pudiéramos desbloquear esas reglas y aplicar ingeniería inversa a la capacidad de la naturaleza para hacer crecer una variedad infinitamente diversa de formas?
Los científicos de la Escuela de Ingeniería y Ciencias Aplicadas (SEAS) de Harvard John A. Paulson han hecho precisamente eso. En un artículo publicado en el procedimientos de la Academia Nacional de Ciencias , un equipo de investigadores de SEAS y el Instituto Wyss de Ingeniería de Inspiración Biológica demuestran una técnica para hacer crecer cualquier forma objetivo a partir de cualquier forma inicial.
"El arquitecto Louis Sullivan dijo una vez que 'la forma siempre sigue a la función', "dijo L. Mahadevan, la Profesora Lola England de Valpine de Matemática Aplicada, de Biología Organísmica y Evolutiva y de Física y autor principal del estudio. "Pero si uno toma la perspectiva opuesta, que tal vez la función debería seguir la forma, ¿Cómo podemos invertir la forma del diseño? "
En investigaciones anteriores, El grupo Mahadevan utilizó experimentos y teoría para explicar cómo las estructuras que se transforman naturalmente, como las trampas de moscas de Venus, piñas y flores:cambiaron de forma con la esperanza de poder algún día controlar e imitar estos procesos naturales. Y de hecho, los experimentalistas han comenzado a aprovechar el poder de patrones de crecimiento bioinspirados. Por ejemplo, en 2016, en colaboración con el grupo de Jennifer Lewis, el profesor Hansjorg Wyss de ingeniería de inspiración biológica en SEAS y miembro principal de la facultad del Instituto Wyss, el equipo imprimió una variedad de estructuras que cambiaron su forma con el tiempo en respuesta a los estímulos ambientales.
"El desafío era cómo resolver el problema inverso, "dijo Wim van Rees, becario postdoctoral en SEAS y primer autor del artículo. "Hay mucha investigación en el lado experimental, pero no hay suficiente en el lado teórico para explicar lo que realmente está sucediendo. La pregunta es, si quiero terminar con una forma específica, ¿cómo diseño mi estructura inicial? "
Inspirado por el crecimiento de las hojas, los investigadores desarrollaron una teoría sobre cómo modelar las orientaciones y magnitudes de crecimiento de una bicapa, dos capas diferentes de materiales elásticos pegadas entre sí que responden de manera diferente a los mismos estímulos. Programando una capa para que se hinche más y / o en una dirección diferente que la otra, la forma general y la curvatura de la bicapa se pueden controlar por completo. En principio, la bicapa puede ser de cualquier material, en cualquier forma, y responder a cualquier estímulo desde el calor hasta la luz, hinchazón, o incluso crecimiento biológico.
El equipo desentrañó la conexión matemática entre el comportamiento de la bicapa y el de una sola capa.
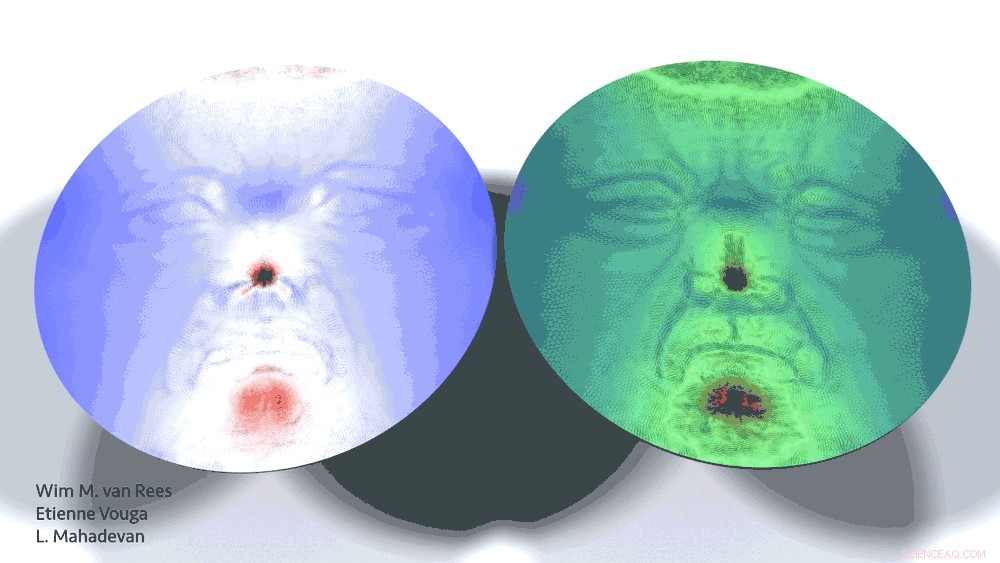
El rostro del padre de la física cuántica, Max Planck, emerge de un disco plano. En cada estado los colores muestran los factores de crecimiento de la capa superior (izquierda) e inferior (derecha), y las delgadas líneas negras indican la dirección de crecimiento. La capa superior se ve desde el frente, y la capa inferior se ve desde atrás, para resaltar la complejidad de las geometrías. Crédito:Harvard SEAS
"Encontramos una relación muy elegante en un material que consta de estas dos capas, ", dijo van Rees." Puede tomar el crecimiento de una bicapa y escribir su energía directamente en términos de una monocapa curva ".
Eso significa que si conoce las curvaturas de cualquier forma, puede aplicar ingeniería inversa a los patrones de energía y crecimiento necesarios para hacer crecer esa forma utilizando una bicapa.
"Este tipo de problema de ingeniería inversa es muy difícil de resolver, incluso usando días de computación en una supercomputadora, "dijo Etienne Vouga, ex becario postdoctoral en el grupo, ahora es profesor asistente de Ciencias de la Computación en la Universidad de Texas en Austin. "Al dilucidar cómo la física y la geometría de las bicapas están íntimamente relacionadas, pudimos construir un algoritmo que resuelve el patrón de crecimiento necesario en segundos, incluso en una computadora portátil, no importa cuán complicada sea la forma del objetivo ".
Los investigadores demostraron el sistema modelando el crecimiento de un pétalo de flor de boca de dragón a partir de un cilindro, un mapa topográfico de la cuenca del río Colorado a partir de una hoja plana y, lo más sorprendente, el rostro de Max Planck, uno de los fundadores de la física cuántica, desde un disco.
"En general, Nuestra investigación combina nuestro conocimiento de la geometría y la física de las carcasas delgadas con nuevos algoritmos matemáticos y cálculos para crear reglas de diseño para la forma de ingeniería. ", dijo Mahadevan." Allana el camino para los avances de fabricación en la impresión 4-D de elementos mecánicos y ópticos que cambian de forma, robótica blanda, así como ingeniería de tejidos ".