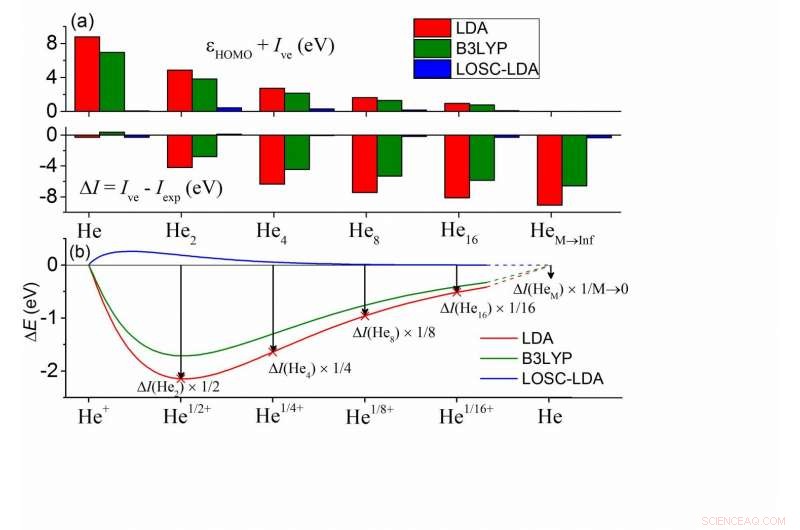
(a) Desviaciones entre el? HOMO y -Ive calculados y entre Ive e Iexp para una serie de grupos de HeM. En cada grupo, todos los átomos de He son químicamente equivalentes. Los átomos vecinos más cercanos están separados por 10Å, y el Iexp de HeM está bien aproximado por Iexp de un átomo de He. (b) Desviación de energía total calculada de la condición de linealidad de un átomo de He con carga fraccionada en función de la carga fraccional δ. Aquí ΔE (Heδ +) =E (Heδ +) - δE (He +) - (1-δ) E (He), y los valores de δ se han escalado en la figura para una comparación directa con (a). Crédito:© Science China Press
La teoría funcional de la densidad de Kohn-Sham es una de las más exitosas en química. Es formalmente riguroso; Su costo computacional relativamente bajo y su precisión competitiva en sistemas pequeños y medianos lo convierten en uno de los métodos más populares en el cálculo de estructuras electrónicas. y quizás la única opción para modelar los efectos cuánticos de los electrones en grandes sistemas químicos y biológicos. Sin embargo, el funcional exacto no se conoce explícitamente y las aproximaciones funcionales de densidad (DFA) del estado de la técnica adolecen de errores sistemáticos. Uno de los errores dominantes en los DFA es el error de deslocalización, que es omnipresente y se manifiesta de diversas formas. Este ha sido un problema abierto desafiante durante décadas. Recientemente, Chen Li, Neil Qiang Su y Weitao Yang de la Universidad de Duke y Xiao Zheng de la Universidad de Ciencia y Tecnología de China desarrollaron un marco novedoso de corrección de escala orbital localizada (LOSC) que demuestra la eliminación sistemática del error de deslocalización.
Las principales consecuencias de los errores de deslocalización en los DFA se pueden clasificar en dos aspectos:(1) error de energía orbital de Kohn-Sham (KS) y (2) error de energía total. El error de deslocalización conduce a fallas importantes en aplicaciones prácticas, como la subestimación no física de los huecos de banda, las distribuciones de electrones excesivamente deslocalizados y las transferencias de carga incorrectas. Con respecto a estos dos aspectos de los errores, ambos se manifiestan de manera dependiente del tamaño. En particular, entre las energías orbitales KS, la energía orbital molecular ocupada más alta (HOMO), εHOMO, se supone que está de acuerdo con el potencial de ionización vertical (negativo) (-Ive), según lo requiera el funcional exacto. Es más, se supone que los Ive calculados por los DFA concuerdan con el valor experimental, Iexp.
Para los DFA de uso común, las dos condiciones no se cumplen. Como se muestra en los cálculos del grupo de helio en la subfigura (a), la energía HOMO por la aproximación de densidad local (LDA) muestra un error positivo en comparación con -Ive mientras que Ive exhibe un error negativo, y los dos errores se muestran en función del tamaño, sugiriendo que el error de deslocalización de los DFA tiene que aparecer de una forma u otra, o ambos, mientras que la suma de las magnitudes permanece sin cambios. Es más, esto es frecuente en todo tipo de DFA, incluyendo el funcional B3LYP más popular, como se muestra en verde.
Para comprender estos errores, los químicos pueden mapearlos en los errores de un átomo de He con carga fraccionada, como se ilustra en la subfigura (b). Se supone que las energías del sistema fraccional se escalan linealmente con el número de electrones fraccionarios n (0? N <1) para el funcional exacto. En la subfigura (b) se muestra la desviación de energía de la condición de linealidad para un solo átomo de He, donde se subestiman las energías fraccionarias del sistema, esto define el error de deslocalización. Es más, el error de carga fraccional en (b) tiene una correspondencia de 1-1 con el error de energía total ΔI =Ive - Iexp. En el límite de M va al infinito, se puede deducir que ΔI está de acuerdo con el error de pendiente de la curva E (N) en el número entero, que es exactamente el error de energía HOMO de un solo átomo de He. Por lo tanto, todos los errores están interconectados. Por tanto, es posible eliminar sistemáticamente el error de deslocalización mediante (1) la eliminación de los errores en (b) y (2) garantizando la eliminación del error de tamaño consistente en todos los sistemas.
En el presente trabajo de LOSC, los autores inventaron variables locales novedosas, llamados orbitallets, que son orbitales localizados (LO) que logran la localidad tanto en espacios espaciales como energéticos. A través de estos orbitallets, pudieron expresar la densidad electrónica y la matriz de densidad KS en la representación local, donde surge naturalmente la matriz de ocupación local compuesta por números fraccionarios. Por lo tanto, estas variables locales son capaces de capturar información fraccionaria local de forma precisa y completa en el espacio orbital, y sirven como los bloques de construcción perfectos para el funcional LOSC. Es más, reescribiendo los términos en las funciones GSC y LSC en términos de fórmulas de corrección de curvatura y haciendo una analogía con la LOSC, introdujeron una matriz de curvatura local, cuyos elementos están diseñados como funcional de los orbitallets, estar en correspondencia uno a uno con la matriz de ocupación local. Finalmente, la fórmula LOSC está escrita como una expresión explícita y elegante sobre el funcional padre en términos de estas dos matrices.
El LOSC logra todas las características deseables. En la figura anterior, los errores LOSC-LDA son esencialmente insignificantes, indicando la validez y consistencia de tamaño de la corrección. Estos también han sido validados por las curvas de disociación mucho mejoradas de los cationes moleculares diatómicos, que van desde H2 +, He2 +, catión dímero de agua y catión dímero de benceno. El HOMO, Los errores de energía de LUMO se han reducido mucho y el buen rendimiento se mantiene a medida que aumenta el tamaño del sistema. Esto se ha demostrado mediante ensayos con oligómeros de poliaceno y trans-poliacetileno. Es más, el LOSC es capaz de recuperar la densidad de electrones correcta cuando los DFA padre lo hacen cualitativamente incorrecto, como se muestra en el ejemplo de un anión de cloro solvatado cuando se le priva de un electrón.
Por tanto, el rendimiento de LOSC promete eliminar sistemáticamente el error de deslocalización dentro de las funciones de densidad de KS. Vale la pena notar que a diferencia del paradigma tradicional de diseñar funcionales usando la densidad, los gradientes de densidad, la densidad de energía cinética, etc., el marco LOSC incluye ingredientes completamente nuevos, los orbitallets, que son funcionales implícitos de la matriz de densidad KS, y demostraron su capacidad única para abordar problemas de larga data asociados con los DFA tradicionales. Esto refleja un cambio de paradigma en el diseño de funcionales, y amplía enormemente el camino en la exploración de lo funcional exacto en su propio espacio vital. En este sentido, LOSC ha marcado el comienzo de la tendencia en el desarrollo de una nueva generación de aproximaciones funcionales de densidad, promover la teoría funcional de la densidad a un nuevo nivel de precisión.