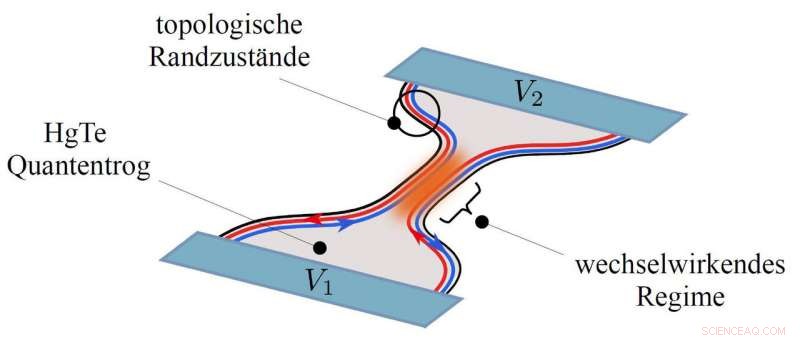
Un pozo cuántico se estrecha en el medio hasta un punto de contacto cuántico. Los físicos de Würzburg han producido este dispositivo utilizando nuevos métodos de nanoestructuración. Crédito:Christoph Fleckenstein / Universidad de Wuerzburg
Los aislantes topológicos son materiales con propiedades asombrosas:la corriente eléctrica fluye solo a lo largo de sus superficies o bordes, mientras que el interior del material se comporta como aislante. En 2007, Profesor Laurens Molenkamp en Julius-Maximilians-Universität (JMU) Würzburg en Baviera, Alemania, fue el primero en demostrar experimentalmente la existencia de tales estados topológicos. Su equipo logró este trabajo fundamental con pozos cuánticos basados en mercurio y telurio (HgTe). Desde entonces, Estos materiales novedosos han sido la esperanza para una generación fundamentalmente nueva de componentes que, por ejemplo, prometen innovaciones para la tecnología de la información.
Los físicos de JMU han logrado por primera vez construir un elemento esencial para tales componentes:un contacto de punto cuántico (QPC). Presentan este logro en una publicación reciente en la revista Física de la naturaleza .
Confinamiento para estados topológicos
Los contactos de puntos cuánticos son constricciones cuasi unidimensionales en estructuras por lo demás bidimensionales que tienen solo unas pocas capas atómicas delgadas. En pozos cuánticos topológicos de HgTe, en el que los estados conductores se encuentran exclusivamente en los bordes, estos estados de borde se fusionan espacialmente en el QPC. Esta proximidad permite investigar posibles interacciones entre los estados de borde.
"Este experimento sólo pudo funcionar gracias a un gran avance en nuestros métodos litográficos. Nos ha permitido crear estructuras increíblemente pequeñas sin dañar el material topológico. Estoy convencido de que esta tecnología nos permitirá encontrar impresionantes, efectos novedosos en nanoestructuras topológicas en un futuro próximo, "dijo Molenkamp.
Comportamiento de conductancia anómalo a través de la interacción
Utilizando un sofisticado proceso de fabricación, los físicos de la JMU han logrado estructurar el cuello de botella con precisión y delicadeza. Este progreso tecnológico les permitió funcionalizar las propiedades topológicas del sistema.
En este contexto, el equipo dirigido por los profesores Laurens Molenkamp y Björn Trauzettel pudo demostrar por primera vez los efectos de interacción entre los diferentes estados topológicos de un sistema utilizando firmas de conductancia anómala. Los investigadores de Würzburg atribuyen este comportamiento particular de los QPC topológicos analizados a la física de los sistemas electrónicos unidimensionales.
Interacción de electrones en una dimensión
Si las correlaciones electrónicas se analizan en una dimensión espacial, los electrones se mueven, a diferencia de dos o tres dimensiones espaciales, de una manera bien ordenada porque no hay posibilidad de "adelantar" al electrón principal. Pictóricamente hablando, los electrones en este caso se comportan como perlas en una cadena.
Esta propiedad especial de los sistemas unidimensionales conduce a interesantes fenómenos físicos. Trauzettel dice:"La interacción de la fuerte interacción de Coulomb y el acoplamiento de la órbita de espín es rara en la naturaleza. Por lo tanto, espero que este sistema produzca descubrimientos fundamentales en los próximos años".
Perspectivas para futuras investigaciones
Los QPC topológicos son un componente elemental para muchas aplicaciones que se han predicho teóricamente en los últimos años.
Un ejemplo particularmente destacado de este tipo es la posible realización de fermiones de Majorana, que el físico italiano Ettore Majorana predijo en 1937. A estas excitaciones se atribuye un potencial de aplicación prometedor en relación con las computadoras cuánticas topológicas.
Para este propósito, es de gran importancia no solo detectar fermiones de Majorana, pero también para poder controlarlos y manipularlos a voluntad. El QPC topológico, implementado por primera vez en JMU Würzburg, ofrece una perspectiva interesante a este respecto.