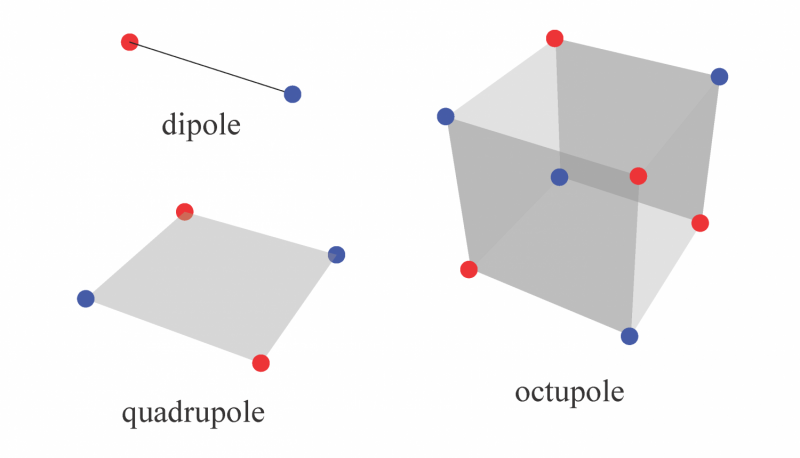
En esta figura, el momento dipolar eléctrico está representado por una carga positiva (punto rojo) y una carga negativa (punto azul) que están separadas espacialmente. El cuadrupolo, compuesto por dos momentos dipolares opuestos, es inherentemente bidimensional, y el octupolo, compuesto por dos cuadrupolos opuestos, es inherentemente tridimensional. Si bien se conocían previamente materiales con momentos dipolares cuantificados, Los cristales aislantes con cuadrupolo cuantificado y momentos octupolares son fases topológicas que no se parecen a ninguna de las descubiertas hasta la fecha. Crédito:Wladimir Balcazar, Departamento de Física e Instituto de Teoría de la Materia Condensada, Universidad de Illinois en Urbana-Champaign.
Investigadores de la Universidad de Illinois en Urbana-Champaign y la Universidad de Princeton han predicho teóricamente una nueva clase de fases aislantes de la materia en materiales cristalinos. señalado dónde se pueden encontrar en la naturaleza, y en el proceso generalizó la teoría cuántica fundamental de las fases de Berry en sistemas de estado sólido. Y lo que es más, estos aislantes generan momentos de cuadrupolo eléctrico u octupolar, que se pueden considerar aproximadamente como campos eléctricos muy específicos, que se cuantifican. Los observables cuantificados son un estándar de oro en la investigación de materia condensada, porque los resultados experimentales que miden estos observables tienen que, en principio, coinciden exactamente con las predicciones teóricas, sin dejar lugar a dudas, incluso en sistemas muy complejos.
La investigación, que es el esfuerzo combinado del estudiante de posgrado Wladimir Benalcazar y el profesor asociado de física Taylor Hughes del Instituto de Teoría de la Materia Condensada de la U. de I., y el profesor de física B. Andrei Bernevig de Princeton, se publica en el 7 de julio, Número 2017 de la revista Ciencias .
El trabajo del equipo comenzó con la identificación de un aislante cuadrupolo, pero pronto se hizo evidente que había implicaciones más profundas.
Benalcázar explica, "Uno de los nuevos modelos que presenta el trabajo tiene un momento cuadrupolo eléctrico cuantificado. Es un aislante diferente a todos los aislantes topológicos conocidos anteriormente. No tiene gapless, estados de superficie de baja energía, el sello distintivo de tales sistemas, que puede ser la razón por la que estos sistemas han evitado ser descubiertos durante tanto tiempo ".
"Pero sorprendentemente, " él continúa, "a pesar de que las superficies del aislante cuadrupolo están abiertas, no son insignificantes. De hecho, ¡Forman una fase aislante topológica de dimensiones inferiores! Nuestros cálculos pueden predecir cuándo un sistema albergará tales aisladores topológicos de límites, ya sea en las superficies, bisagras o esquinas. Asombrosamente, esta propiedad en su forma más básica está relacionada con los momentos multipolares eléctricos superiores ".
Obra revolucionaria de Vanderbilt en las décadas de 1990 y 2000, King-Smith, Resta, Martín, Ortiz, Marzari, y Souza, hizo posible definir el momento dipolar de un cristal a través de una aplicación particular de la fase de Berry, una cantidad matemática que caracteriza la evolución de las funciones de onda de los electrones en el espacio de momento de la red. Ese trabajo representó un gran avance en nuestra comprensión de los fenómenos electromagnéticos topológicos en materiales cristalinos. Proporcionó un vínculo entre una cantidad física (momento dipolar) y una topológica (fase de Berry). Según Hughes y Bernevig, La investigación actual comenzó como un esfuerzo por generalizar la teoría del momento dipolar a momentos multipolares superiores.
Hughes cuenta:"En las primeras etapas, Andrei y yo estábamos discutiendo la idea de extender el trabajo sobre momentos dipolares cristalinos a momentos cuadrupolos. Pero resulta que mientras que la pregunta parecía algo obvia una vez formulada, la solución matemática no lo era. Calcular momentos multipolares en un sistema mecánico cuántico de electrones es un desafío porque el electrón, una partícula de mecánica cuántica, es una ola, no solo una partícula, y su ubicación en el espacio es incierta. Mientras que se puede acceder al momento dipolar midiendo solo el desplazamiento del electrón, una cantidad vectorial, los momentos de cuadrupolo son más complicados ".
Para abordar esto, los científicos tuvieron que inventar un nuevo marco teórico. Además, necesitaban construir modelos con las propiedades adecuadas mediante las cuales pudieran comparar su nueva técnica analítica. Pero, de hecho, las cosas sucedieron en el orden opuesto:Hughes y Bernevig le dan crédito a Benalcázar por haber encontrado el modelo correcto, una generalización de un aislante dipolo con un momento dipolar cuantificado. Desde allí, tomó un año entero construir el marco teórico completo.
Las herramientas matemáticas existentes, las fases de Berry en estado sólido, solo podían resolver la posición del electrón en una dirección a la vez. Pero para el momento del cuadrupolo, el equipo necesitaba determinar su posición en dos dimensiones simultáneamente. La complicación se deriva de la
Principio de incertidumbre de Heisenberg, que generalmente establece que no se pueden medir la posición y el momento de un electrón al mismo tiempo. Sin embargo, en los nuevos aisladores cuadrupolos, un principio de incertidumbre diferente está en funcionamiento, impidiendo la medición simultánea de la posición del electrón en las direcciones X e Y. Debido a esto, los autores no pudieron resolver espacialmente las ubicaciones de los electrones utilizando las herramientas teóricas existentes.
"Podríamos precisarlo en una dirección, pero no el otro, "Recuerda Benalcázar." Para obtener ambas direcciones simultáneamente, creamos un nuevo paradigma analítico, esencialmente separando el momento cuadrupolo en un par de dipolos ".
Hughes agrega, "En primer lugar, Hicimos todas las pruebas que sabíamos cómo ejecutar en los modelos que propusimos y seguimos sin encontrar nada. El problema es, cuando dos dipolos están uno encima del otro, se anulan mutuamente. Para ver el cuadrupolo, necesita cierta resolución espacial para determinar si los dipolos están realmente separados. Al final resultó que necesitábamos mirar las fases de Berry una capa más profunda, matemáticamente hablando ".
Encontrar una manera de resolver espacialmente esa segunda dimensión representa un avance teórico significativo. Los autores idearon un nuevo paradigma para calcular la ubicación de los electrones que es una extensión de la formulación de la fase Berry. Primero, utilizan una técnica convencional para dividir teóricamente la onda de electrones en dos nubes de carga, separados en el espacio. Luego muestran que cada nube tiene un momento dipolar. Este de dos pasos, procedimiento anidado puede revelar dos espacialmente separados, dipolos opuestos:un cuadrupolo.
Bernevig comenta, "Los aislantes topológicos a los que nos hemos acostumbrado en la última década se describen esencialmente mediante un procedimiento matemático llamado tomar la fase Berry de algunos estados electrónicos. La fase Berry del interior de una muestra, en efecto, conoce el borde de un sistema; puede decirle qué es interesante acerca del borde.
Para ir un paso más allá y resolver lo que es potencialmente notable en la esquina de un sistema o muestra, Usted tiene que tomar, en efecto, una fase Berry de una fase Berry. Esto conduce a la formulación de una nueva cantidad topológica que describe el momento cuadrupolo cuantificado ".
En la ultima década, la clasificación de las fases topológicas de la materia se ha desarrollado sustancialmente. Significativamente, este nuevo trabajo muestra la riqueza aún inexplorada del campo. Predice una clase de fases completamente nueva y proporciona el modelo y los medios teóricos para probar su existencia. Quizás uno de los aspectos más interesantes del campo de los aislantes topológicos es su relevancia experimental. En el artículo de la revista, el equipo sugiere tres posibles configuraciones experimentales para validar su predicción.
Hughes reconoce que una simulación cuántica, una técnica experimental que, por ejemplo, utiliza láseres finamente ajustados y átomos ultrafríos para replicar y sondear las propiedades de materiales reales; sería el más accesible de inmediato.
"Es emocionante que utilizando tecnología experimental actual, nuestro modelo se puede ver de inmediato, ", Afirma Hughes." Esperamos que nosotros o alguien más finalmente encontremos un material de estado sólido con este tipo de cualidades. Pero eso es desafiante todavía no tenemos una fórmula química ".
Los autores indican que las condiciones para conseguir este efecto son bastante generales, y como tal, hay muchos candidatos potenciales en muchas clases de materiales.
"O la comprensión podría llegar algún día desde el jardín izquierdo, de alguna otra idea de implementación completamente ingeniosa que alguien podría idear, ", Bromea Bernevig.
Benzalcázar está convencido de que "este nuevo entendimiento puede abrir toda una colección de materiales que tengan esta clasificación jerárquica".
Esta es una investigación fundamental, y cualquier aplicación potencial es todavía una cuestión lejana de conjeturas. Debido a que los observables cuantificados permiten mediciones exquisitamente precisas, Es concebible que las nuevas propiedades eléctricas de esta nueva fase de la materia sean útiles en metrología, tecnologías electrónicas, o en el diseño de materiales con propiedades prescritas de volumen / superficie / borde / esquina.
Los autores están de acuerdo, este trabajo abre muchas posibilidades para nuevos sistemas topológicos que estaban ocultos antes, ocultos dentro de la estructura anidada de las matemáticas de la fase Berry. Estas fases topológicas ocultas tienen una fuerte conexión con los observables físicos reales, y puede haber otros fenómenos físicos en estos materiales que serían interesantes de explorar.