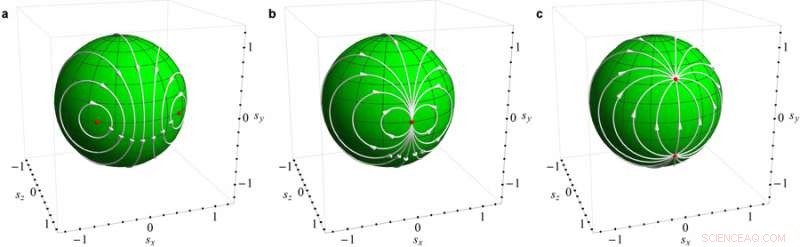
Dos físicos de Argonne ofrecieron una forma de describir matemáticamente un fenómeno físico particular llamado transición de fase en un sistema fuera de equilibrio (es decir, con energía moviéndose a través de él) mediante el uso de números imaginarios. La ilustración relaciona la transición de fase con el cambio entre transformaciones matemáticas de Mobius (a, B, y C). La teoría de la física del desequilibrio es un objetivo buscado desde hace mucho tiempo en el campo, y eventualmente podría ayudarnos a diseñar mejores dispositivos electrónicos. Crédito:Laboratorio Nacional Vinokur / Galda / Argonne
Los números imaginarios son una solución a un problema muy real en un estudio publicado hoy en Informes científicos .
Dos físicos del Laboratorio Nacional Argonne del Departamento de Energía de EE. UU. Ofrecieron una forma de describir matemáticamente un fenómeno físico particular llamado transición de fase en un sistema fuera de equilibrio. Tales fenómenos son fundamentales en la física, y comprender cómo ocurren ha sido un objetivo inquietante desde hace mucho tiempo; su comportamiento y los efectos relacionados son clave para abrir posibilidades para la nueva electrónica y otras tecnologías de próxima generación.
En física, "equilibrio" se refiere a un estado en el que un objeto no está en movimiento y no tiene energía fluyendo a través de él. Como se podría esperar, la mayor parte de nuestras vidas transcurren fuera de este estado:nos movemos constantemente y hacemos que otras cosas se muevan.
"Una tormenta, este ventilador giratorio, todos estos sistemas están fuera de equilibrio, "dijo el coautor del estudio de Valerii Vinokur, un Argonne Distinguished Fellow y miembro del Instituto de Computación conjunto Argonne-University of Chicago. "Cuando un sistema está en equilibrio, sabemos que siempre está en su configuración de energía más baja posible, pero para el desequilibrio este principio fundamental no funciona; y nuestra capacidad para describir la física de tales sistemas es muy limitada ".
Él y el coautor Alexey Galda, científico de Argonne y del Instituto James Franck de la Universidad de Chicago, había estado trabajando en formas de describir estos sistemas, particularmente aquellos que experimentan una transición de fase, como el momento durante una tormenta cuando la diferencia de carga entre la nube y el suelo se inclina demasiado alta, y ocurre un rayo.
Encontraron su nuevo enfoque de la física del no equilibrio en una nueva rama de la mecánica cuántica. En el lenguaje de la mecánica cuántica, la energía de un sistema está representada por lo que se llama un operador hamiltoniano. Tradicionalmente, La mecánica cuántica había sostenido que el operador para representar el sistema no puede contener números imaginarios si eso significaría que la energía no aparece como un valor "real" y positivo, porque el sistema realmente existe en la realidad. Esta condición se llama hermiticidad.
Pero los físicos han estado analizando más detenidamente a los operadores que violan la hermiticidad mediante el uso de componentes imaginarios, Vinokur dijo; varios de estos operadores descubiertos hace unos años se utilizan ahora ampliamente en óptica cuántica.
"Notamos que estos operadores son una hermosa herramienta matemática para describir procesos fuera de equilibrio, " él dijo.
Para describir la transición de fase, Galda y Vinokur escribieron al operador hamiltoniano, introdujo una fuerza aplicada para sacarlo del equilibrio, y luego hicieron la fuerza imaginaria.
"Este es un truco que es ilegal desde cualquier punto de vista del sentido común; pero vimos que esta combinación, energía más fuerza imaginaria, describe perfectamente matemáticamente la dinámica del sistema con fricción, "Dijo Vinokur.
Aplicaron el truco para describir otras transiciones de fase fuera de equilibrio, como una transición dinámica de Mott y un sistema de giro, y vio que los resultados coincidían con los experimentos observados o con las simulaciones.
En su último trabajo, conectaron su descripción con una operación llamada transformación de Möbius, que aparece en una rama de las matemáticas llamada topología. "Podemos entender las transiciones de no equilibrio ahora como transiciones topológicas en el espacio de la energía, "Dijo Galda.
Esta pequeña travesura cuántica debe entenderse más profundamente, ellos dijeron, pero es valioso de todos modos; la teoría describe áreas básicas de la física que son de gran interés para la tecnología electrónica de próxima generación.
"Por el momento, la conexión con la topología parece un caramelo matemático, algo hermoso que aún no podemos usar, pero sabemos por la historia que si las matemáticas son lo suficientemente elegantes, muy pronto siguen sus implicaciones prácticas, "Dijo Vinokur.