
Esta película de jabón contenida dentro de una varilla de metal tiene uniones donde se encuentran varias películas de jabón. En 2014, La profesora Jenny Harrison de UC Berkley amplió la solución al problema de Plateau para dar cuenta de formas más complicadas de películas de jabón como esta. Crédito:Instituto de Ciencia y Tecnología de Okinawa
A menudo se usa para la diversión de los niños, las pompas de jabón son delicadas, películas que reflejan la luz que normalmente duran solo unos segundos antes de estallar. Pero más allá de su valor para entretener, las pompas de jabón son ejemplos físicos del rico problema matemático de las superficies mínimas; asumen la forma de la menor superficie posible, que contiene un volumen dado. Investigadores de la Universidad de Graduados del Instituto de Ciencia y Tecnología de Okinawa (OIST, por sus siglas en inglés) han resuelto recientemente la solución a un problema matemático, conocido como el problema Kirchhoff-Plateau, que se ilustra simplemente con películas de jabón que abarcan bucles flexibles.
"Nuestra solución del problema de Kirchhoff-Plateau trae hermosos resultados matemáticos cercanos a lo que sucede en el mundo físico, "dice el Dr. Giulio Giusteri, coautor del artículo que se publicó recientemente en el Journal of Nonlinear Science. El Dr. Giusteri trabajó con el profesor Eliot Fried, quien dirige la Unidad Matemática de Materia Blanda de la OIST, y el Dr. Luca Lussardi de la Università Cattolica del Sacro Cuore en Italia.
La pregunta respondida por el equipo es una variante del "Problema de meseta", un problema matemático de siglos de antigüedad, lleva el nombre de un físico belga del siglo XIX, Joseph Plateau. Plateau planteó la hipótesis de que cuando sumerges un marco de alambre rígido en una solución de jabón, la superficie de la película de jabón formada en el marco representa un área mínima matemáticamente posible, no importa la forma del marco.
La primera solución satisfactoria para el problema de Plateau se proporcionó en el siglo XX, por el matemático estadounidense Jesse Douglas, por lo que fue galardonado con la Medalla Fields en 1936. Más recientemente, en 2014, La profesora Jenny Harrison de UC Berkeley amplió el trabajo de Douglas, proporcionar una prueba válida bajo hipótesis generales que abarquen, por ejemplo, situaciones en las que hay uniones en las que se encuentran varias películas de jabón.
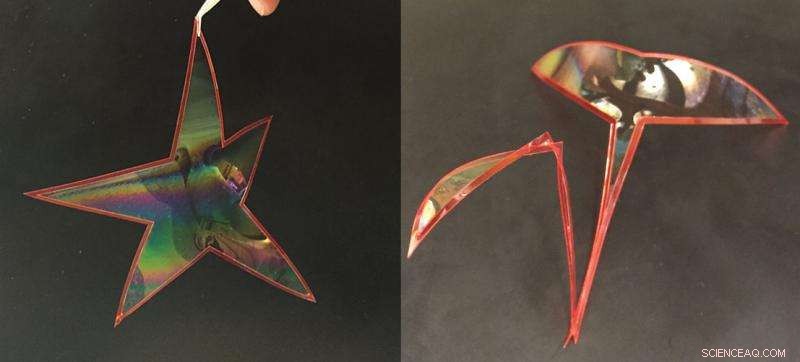
Las películas de jabón contenidas dentro de un bucle flexible ejercen una fuerza sobre el bucle, haciendo que cambie de forma. Por ejemplo, el mismo lazo puede formar una estrella o un cisne dependiendo de la tensión superficial de la película de jabón. Crédito:Instituto de Ciencia y Tecnología de Okinawa
En contraste con el problema de Plateau en el que una película de jabón se extiende por un marco fijo, el problema de Kirchhoff-Plateau se refiere a las formas de equilibrio de las películas de jabón que se extienden por bucles flexibles, hecha, por ejemplo, de hilo de pescar, que se puede describir utilizando la teoría de varillas de Kirchhoff, un modelo que proporciona un enfoque poderoso para estudiar la estática y la dinámica de varillas elásticas delgadas. La complicación es que un bucle flexible puede cambiar de forma en respuesta a la fuerza ejercida por la película de jabón. Como tal, Una solución al problema requiere determinar no solo la forma de la película de jabón, sino también la forma del lazo delimitador. A diferencia de, la forma del límite en el problema original de Plateau es conocida porque está hecha de alambre rígido que permanece fijo contra las fuerzas relativamente débiles de la película de jabón.
Una complicación adicional asociada con el problema de Kirchhoff-Plateau es que, a diferencia del problema original de Plateau, en el que se supone que el límite es unidimensional, una vara de Kirchhoff es un objeto tridimensional. Aunque los filamentos como el hilo de pescar son delgados, son órdenes de magnitud más gruesas que una película de jabón en equilibrio, lo que significa que el área de la película de jabón puede cambiar dependiendo del punto en el que la película entra en contacto con el bucle.
Los investigadores tradujeron con éxito todos estos efectos físicos en términos matemáticos. Como explica el profesor Fried:"No importa qué tan fuerte sea la competencia entre la tensión superficial de la película de jabón y la respuesta elástica del bucle, el sistema siempre puede ajustarse para lograr una configuración de menor energía ".
La solución al problema de Kirchhoff-Plateau no solo contribuye a la comprensión de la energía minimizando las formas matemáticas, pero también se puede aplicar a sistemas biológicos. Por ejemplo, podría ayudarnos a comprender cómo la forma de una proteína determina cómo interactúa y se une a una superficie.
El equipo ahora está trabajando en simulaciones por computadora que, basado en este modelo matemático, Puede predecir el comportamiento de los sistemas físicos.