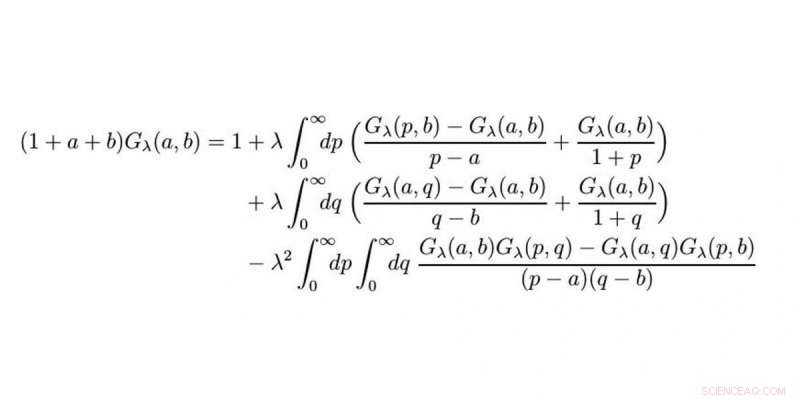
La ecuación matemática. Crédito:WWU / Raimar Wulkenhaar
Después de 10 años, El profesor Raimar Wulkenhaar del Instituto de Matemáticas de la Universidad de Münster y su colega el Dr. Erik Panzer de la Universidad de Oxford han resuelto una ecuación matemática que se consideraba irresoluble. La ecuación se utilizará para encontrar respuestas a las preguntas planteadas por la física de partículas elementales. En esta entrevista con Christina Heimken, Wulkenhaar recuerda los desafíos encontrados al buscar la fórmula para una solución y explica por qué el trabajo aún no está terminado.
Trabajó en la solución de la ecuación durante 10 años. ¿Qué hizo que esta ecuación fuera tan difícil de resolver?
Es una ecuación integral no lineal con dos variables. Una ecuación de este tipo es tan compleja que en realidad piensas que no puede haber ninguna fórmula para una solución. Dos variables por sí solas son un desafío en sí mismas, y no existen enfoques establecidos para encontrar una solución para ecuaciones integrales no lineales. Sin embargo, una y otra vez durante esos 10 años hubo destellos de esperanza y, como resultado, y a pesar de todas las dificultades, Pensé que encontrar una fórmula explícita para una solución, expresada a través de funciones conocidas, era realmente posible.
¿Para qué se puede usar la ecuación?
Se trata de una comprensión matemática de las teorías cuánticas de campos. Pertenecen al campo de la física y participan en experimentos a gran escala como los llevados a cabo en el CERN. El objetivo es describir matemáticamente partículas elementales, es decir, los componentes más pequeños conocidos de la materia. Pero esto es tan complicado que, en lugar de, Las partículas imaginarias se describen matemáticamente que tienen ciertas propiedades de las partículas reales. La esperanza es que algún día las partículas reales puedan describirse utilizando los métodos establecidos de esta manera.
Después de trabajar en el problema durante 10 años, experimentó un gran avance este año. ¿Cómo surgió la idea?
Hacia finales de mayo, Probé una idea para la cual mi Ph.D. estudiante, Alexander Hock, proporcionó el impulso decisivo. Desarrollé una nueva ecuación, más simple que la anterior, y comencé a resolverla en ciclos. Lo que esto significa es que te acercas a la solución paso a paso, es decir, bucle por bucle, calculando el lado izquierdo de la ecuación en cada paso anterior y usándolo para el lado derecho de la ecuación en el siguiente paso.
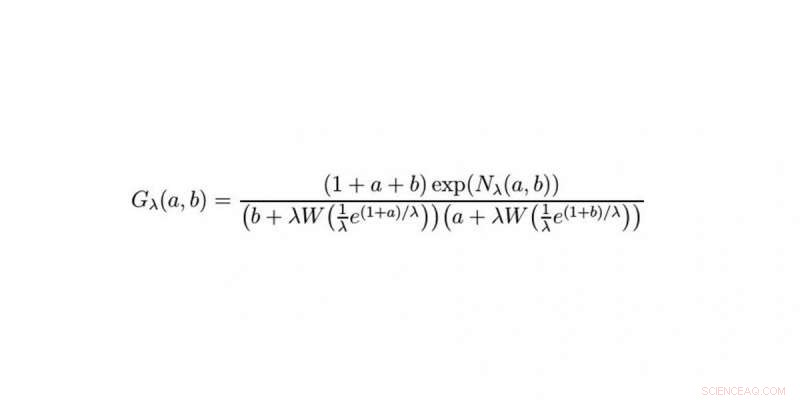
La solución. Crédito:WWU / Raimar Wulkenhaar
En el cuarto ciclo tuve que calcular una suma de 46 integrales que contenían, entre otras cosas, polilogaritmos. Estos polilogaritmos, cuáles son algunas de las funciones más exigentes, se volvió más complicado en cada bucle. Tuve suerte en eso en suma, casi todo se anuló, y lo que quedaba era sólo una pequeña suma de potencias de logaritmos normales. Inmediatamente me di cuenta de que había un tesoro que se podía encontrar aquí.
El quinto bucle no fue tan fácil de resolver, pero nuevamente tuve suerte. Durante una escuela de verano en los Alpes franceses tuve la oportunidad de hablar con expertos sobre tales funciones. Uno de estos expertos fue el Dr. Erik Panzer de la Universidad de Oxford. Había escrito un programa de computadora sobre las matemáticas simbólicas de los hiperlogaritmos y brindó apoyo. De la noche a la mañana, este programa calculó mi ecuación hasta el séptimo ciclo. Confirmó mis resultados hasta el cuarto ciclo, y después del cuarto ciclo, el milagro continuó:todo podía descomponerse en logaritmos normales. ¡Comenzó a surgir un patrón!
¿Qué significa eso?
Quizás recuerdes el Triángulo de Pascal de tus días escolares, con los coeficientes binominales? En el triangulo cada número ingresado en una línea del triángulo es la suma de los dos números ingresados arriba. Y es una estructura tan triangular la que encontramos en nuestros bucles, aunque más complicada que en el triángulo de Pascal.
El 9 de junio se completaron los bucles ocho y nueve. Y luego llegó el que quizás fue el momento más importante. Erik Panzer descifró una fórmula llamada recursiva, que genera cada última línea del triángulo a partir de la línea superior, y que así nos permite extrapolar de lo conocido a lo desconocido.
¿Qué pasó por tu mente en este momento?
Una de las cosas que pensé fue "Nadie puede tener tanta suerte". Me di cuenta de que resolveríamos la ecuación. En nuestra cena había una botella de vino para nuestra mesa ...
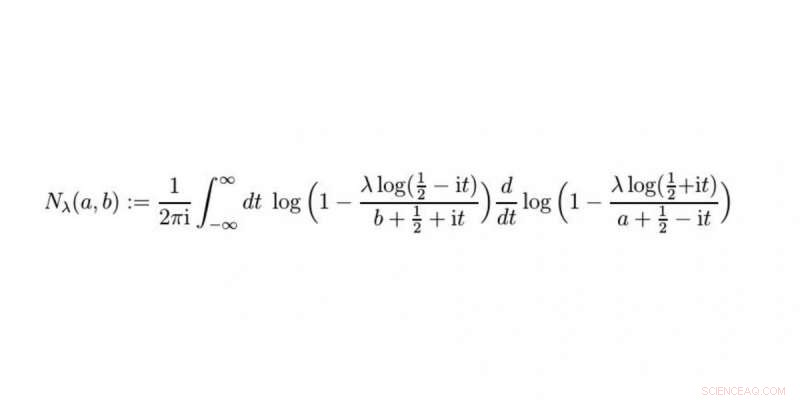
La función de Nielsen es parte de la solución. El Prof. Raimar Wulkenhaar y el Dr. Erik Panzer descubrieron esta nueva función en el transcurso de su trabajo. Crédito:WWU / Raimar Wulkenhaar
… Antes de volver al trabajo.
Si. Al día siguiente logré reducir parte de la ecuación a una simple serie de derivadas. Inicialmente, el resto parecía difícil. No fue hasta altas horas de la noche que se me ocurrió la idea de utilizar la fórmula de Cauchy para resolverlo. Configuré mi despertador para las 5:30 de la mañana siguiente y lo probé de inmediato. Funcionó en el primer intento, y en el siguiente paso encontré una fórmula que había visto a menudo. Sabía que se resolvería usando la función Lambert W. Unos minutos más tarde recibí un correo electrónico de Erik Panzer:él también había pensado en la función de Lambert, pero por una ruta completamente diferente. Como resultado, logramos algo que no había sido factible durante 10 años:la solución de la ecuación integral que describe el modelo de una teoría cuántica de campos. Fue simplemente increíble.
Utiliza ideas y métodos desarrollados por matemáticos en el siglo XVIII que hoy en día se han olvidado casi por completo.
Estas viejas fórmulas nos ayudaron mucho. La función Lambert W, que es una parte elemental de nuestra solución, lleva el nombre del matemático suizo Johann Heinrich Lambert. Esta ecuación se presenta en una gran cantidad de preguntas completamente diferentes. Debido a la falta de conocimiento del trabajo preliminar de Lambert, la función de Lambert se inventó una y otra vez, y se estableció como estándar en 1993. También usamos la fórmula de Lagrange-Bürmann, que nos ayudó a resolver una integral con la ayuda de la función de Lambert, así como la fórmula de Cauchy. En general, las matemáticas tienen mucho respeto por sus antepasados. Nombres como Euler, Lambert, Lagrange, Cauchy, Se cita a Gauss y Hilbert con el mayor reconocimiento por sus logros. Pero hay dos herramientas modernas de las que no querría prescindir:Wikipedia y el álgebra informática. Puede encontrar información completa en Wikipedia que cubre estructuras y funciones matemáticas conocidas (y menos conocidas). Las computadoras pueden resolver ecuaciones incomparablemente más rápido que a mano, y sin cometer errores
¿Cuáles son los siguientes pasos?
Se produce una nueva función en nuestra solución a la que hemos denominado función de Nielsen. Cuando lo hemos entendido mejor y hemos resuelto, por ejemplo, cómo se relaciona con otras funciones conocidas, enviaremos nuestro trabajo, que es de libre acceso en línea como una preimpresión, para su publicación en una revista especializada con revisiones por pares.
Después de eso, me gustaría continuar con el trabajo en el que he estado involucrado desde 2002 con mi colega el Prof. Harald Grosse de Viena. Se trata de una teoría cuántica de campos para partículas matemáticas. Ahora podremos comprender completamente este modelo con la ayuda de la ecuación que hemos resuelto.