
Origami computacional de ingeniería inversa para envoltura conforme. (A) Las arrugas se forman cuando se envuelve firmemente una hoja de papel rectangular alrededor de una superficie gaussiana distinta de cero. (B) Los patrones de corte fractal pueden evitar las arrugas, pero conducen inevitablemente a aberturas y áreas descubiertas. (C) El despliegue 2D de un poliedro esférico generado automáticamente por origami computacional puede envolver una bola de acero sin dejar áreas descubiertas. (D) A medida que aumenta el número de facetas, la suavidad y adaptabilidad de la malla mejoran naturalmente. La diferencia en el área de la superficie entre la esfera perfecta y los poliedros aproximados disminuye en un 5.3% cuando el número de facetas aumenta de 80 a 500. La distancia de Hausdorff entre las superficies poliédricas y la esfera perfecta también se reduce de 7.05 a 1.17% del radio de la esfera perfecta cuando el número de facetas aumenta de 80 a 500 (Crédito de la foto:Y.-K. Lee, Universidad Nacional de Seúl). Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
La pregunta contradictoria sobre cómo envolver una superficie esférica curva utilizando materiales convencionalmente rígidos y no estirables o quebradizos, constituye la base de este estudio. Para responder a la pregunta, Yu-Ki Lee y un equipo de investigación en los departamentos de ingeniería de materiales e informática en la República de Corea y los EE. UU. Extendieron un método de diseño geométrico de origami computacional para envolver construcciones esféricas en un nuevo informe ahora publicado en Avances de la ciencia . El enfoque proporcionó un método robusto y confiable para diseñar dispositivos conformados para superficies curvas arbitrarias utilizando una red desarrollable no poliédrica diseñada computacionalmente. El diseño asistido por computadora transformó materiales bidimensionales (2-D) como obleas de silicio (Si) y láminas de acero en estructuras conformadas que podrían envolver completamente las estructuras 3-D sin fracturas o deformaciones. El método de envoltura computacional les permitió desarrollar una plataforma de diseño para transformar dispositivos 2-D convencionalmente no estirables en superficies curvas 3-D conformadas.
El estudio introdujo un método universal para materiales no estirables convencionales para envolver superficies curvas en 3D arbitrarias y diversas mediante la ingeniería de dispositivos de material conformado sin sacrificar su rendimiento. Por ejemplo, envolver una esfera con un trozo de papel rectangular inevitablemente puede formar arrugas, mientras se intenta envolver una esfera con un sustrato más duro, el material de envoltura puede fracturarse. Para facilitar el proceso, los científicos de materiales pueden introducir cortes con patrones en los materiales no estirables, incluyendo patrones de corte de celosía y patrones de corte fractal para envolver eficazmente superficies 3D. Dichos conceptos se pueden programar en forma y pueden cubrir una esfera de manera eficiente. Los ingenieros también han recomendado algoritmos informáticos para diseñar modelos tridimensionales complejos basados en estructuras auxéticas bidimensionales. Para lograr una cobertura óptima, introdujeron una estrategia de diseño computacional conocida como "envoltura computacional con redes desarrollables no poliédricas, "para formar plataformas de material no extensibles para wearables y dispositivos conformes.
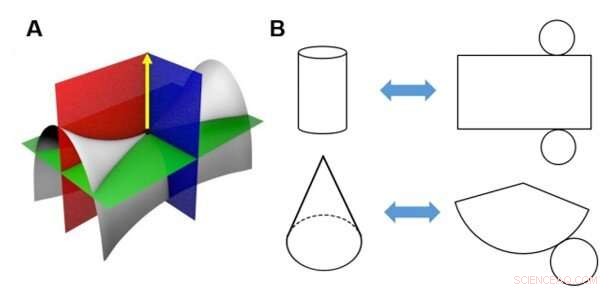
Limitación matemática de envolver una hoja plana alrededor de una superficie 3D con curvaturas gaussianas distintas de cero. (A) La curvatura gaussiana es el producto vectorial de las curvaturas principales máxima y mínima en un punto. En el punto de silla (punto negro) de la superficie gris, una de las principales curvaturas es la intersección entre las superficies roja y gris, y el otro es la intersección entre las superficies azul y gris. Tanto el plano rojo como el azul contienen el vector normal del punto silla, y sus intersecciones con la superficie gris definen las principales curvaturas. Un material 2D con cero puntos de curvatura gaussiana, como una hoja de papel, se denomina "superficie desarrollable", que no se puede transformar en una superficie 3D con una curvatura gaussiana positiva o negativa (es decir, una "superficie no desarrollable") sin estirar ni comprimir. (B) Por ejemplo, un cilindro o un cono se puede cubrir con papel cortado, pero una silla de montar o una esfera no se puede envolver sin que se formen arrugas o cortes. El proceso inverso (aplanamiento) también es el mismo, por eso hay distorsiones en el mapa plano de la Tierra. Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
En teoria, los investigadores pueden caracterizar una superficie curva por la curvatura gaussiana, que es el producto vectorial de las curvaturas principales máxima y mínima en un punto. Por ejemplo, una hoja de papel se denomina "superficie desarrollable" y representa un material 2-D con curvatura gaussiana cero en todos los puntos. Una superficie desarrollable no se puede transformar en una superficie 3D no desarrollable sin romperse, estirar o comprimir el material. El concepto está matemáticamente probado por el "Gauss Theorema Egregium, "que establece que" Para mover una superficie a otra superficie, la curvatura gaussiana de todos los puntos correspondientes debe coincidir ". Los científicos informáticos han realizado grandes esfuerzos para determinar algorítmicamente cortes de superficie que segmentan una superficie no desarrollable en parches de superficie desarrollables conocidos como redes poliédricas o simplemente— Los métodos computacionales recientes tienen como objetivo optimizar la calidad de la red y la capacidad de plegado mediante métodos de aprendizaje automático para reducir el tiempo y el esfuerzo necesarios para los enfoques tradicionales de prueba y error.
Dado que la mayoría de los objetos tridimensionales del mundo real son suaves y curvos, los científicos necesitan mallas de alta resolución para cubrir las superficies con precisión. En este trabajo, Lee y col. desarrolló un nuevo enfoque conocido como "envoltura computacional" que va más allá del método convencional de plegado computacional. Para lograr esto, consideraron el diseño de dispositivos conformes como un problema de envoltura de papel en lugar de un desafío de plegado de papel (origami). El equipo reconoció las funciones de unir y envolver dispositivos conformados para cubrir una superficie 3-D curva subyacente, simplemente doblando y presionando una red poliédrica sin arrugas.

Concepto y demostración física de envoltura computacional. (A) Cuando se minimiza la suma de los ángulos de plegado de una red, las líneas de pliegue se pueden ignorar para adaptarse a materiales rígidos y quebradizos flexibles pero que no se pueden estirar. Para 500 mallas, los huecos en el caso de un material rígido y las arrugas en el caso de un material flexible ya no son visibles, y la diferencia entre los dos se vuelve imperceptible. (B) Una hoja de acero inoxidable no extensible se corta en una red desarrollable. (C) Con un número suficiente de mallas, la hoja de acero inoxidable se puede doblar y envolver completamente una esfera sin arrugar ni doblar. (D) Parte de la esfera se despliega con 400 mallas, y se eliminan las arrugas. (E) Una oblea de Si quebradizo de 20 μm de espesor se corta en una red desplegada con un cortador láser. (F) La oblea de Si cortada envuelve de forma estable los marcos convexos y cóncavos. (Crédito de la foto:Y.-K. Lee, Universidad Nacional de Seúl). Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
Las mallas de alta resolución les permitieron abordar los límites de los largos tiempos de fabricación y la confiabilidad mecánica. Para encerrar una superficie con una curvatura gaussiana completa distinta de cero, como una esfera perfecta, Lee y col. usó una superficie desarrollable después de refinar la malla de facetas para cumplir con los valores requeridos de hermeticidad de envoltura. Los resultados proporcionaron datos sobre una red desarrollable no poliédrica para crear espacios controlados y delimitados entre la red y la esfera sin espacios ni superposiciones entre las facetas. El proceso de fabricación produjo con precisión superficies 3D altamente complejas y lisas muchas veces más rápido que los métodos de plegado computacional convencionales cuando se manejan formas complejas usando papel. materiales de envoltura metálicos y cerámicos. El análisis de elementos finitos apoyó que tales envolturas computacionales eran mecánicamente confiables.

Simulación de elementos finitos (FE) para envolver una esfera con una oblea de Si de 100 µm de espesor con una red desarrollable no poliédrica. Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
Las estructuras desarrolladas en el trabajo llevaron a un aumento significativo en el origami computacional para los procesos de fabricación industrial del mundo real. Por ejemplo, Lee y col. desarrolló un dispositivo conformado usando paneles de lámpara electroluminiscente (EL) para envolver una esfera, el dispositivo conformado tridimensional resultante mostró una buena función y atribuyeron los resultados a los procesos de doblado y prensado utilizados para envolver la esfera en lugar de las técnicas de doblado y plegado. El equipo también demostró de manera similar su método en una máscara coreana comercial y en un vehículo de juguete eléctrico con paneles EL adjuntos para funcionar sin fallas. Generar la red desarrollable para componentes con superficies gaussianas distintas de cero como los faros del vehículo eléctrico de juguete, los científicos utilizaron el método de despliegue del algoritmo genético (GA).

Demostración de dispositivos conformados. (A) Cortable, no estirable Los paneles EL comerciales que consisten en electrodos quebradizos se cortan con un cortador láser para formar redes desarrollables para una esfera. (B) Los paneles EL con una red desarrollable pueden cubrir completamente una esfera y (C) operar sin fallas catastróficas. (D y E) El concepto de envoltura computacional también se demuestra para un modelo elipsoide. (F y G) Además de una esfera y un elipsoide, una mascarilla facial coreana comercial también se puede cubrir de forma cómoda con paneles EL y operar sin fallas eléctricas. (H) Un vehículo eléctrico de juguete también se puede envolver de forma cómoda con paneles EL de la misma manera, y los paneles EL adjuntos también funcionan bien sin fallas. El método de despliegue GA se utiliza para generar la red desarrollable para piezas con superficies gaussianas distintas de cero, incluyendo (I) los faros, el borde del parachoques lateral delantero, y (J) el borde del parachoques lateral trasero del vehículo eléctrico de juguete. (Crédito de la foto:Y.-K. Lee, Universidad Nacional de Seúl.) Crédito:Science Advances, doi:10.1126 / sciadv.aax6212
De este modo, Yu-Ki Lee y sus colegas introdujeron el concepto de envoltura computacional para convertir dispositivos flexibles 2-D no extensibles en dispositivos conformados 3-D. Usando el método, encerraron una superficie con una curvatura gaussiana distinta de cero, como una esfera perfecta. La técnica propuesta podría controlar la distancia entre las dos superficies para asegurar un envoltorio ajustado. El trabajo produjo una sola superficie conectada conocida como red desarrollable no poliédrica, diseñado para envolver conforme a una hoja 2-D para cualquier superficie 3-D. Como resultado, los científicos incluso pudieron facilitar materiales rígidos y quebradizos, como láminas de metal y obleas de Si, para cubrir y envolver completamente superficies de curvatura gaussiana distinta de cero. El método de envoltura computacional universal desarrollado en este trabajo proporcionará nuevos conocimientos sobre el desarrollo de dispositivos conformes con formas arbitrarias utilizando algoritmos eficientes y robustos, métodos de fabricación fiables.
© 2020 Science X Network