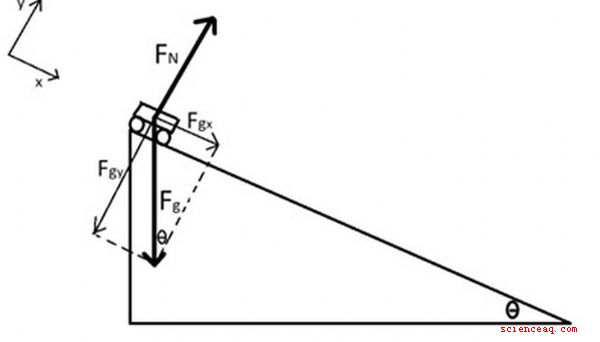
La fuerza neta La primera ley de Newton establece que un objeto que experimenta un movimiento uniforme, lo que significa que está en reposo o se mueve con velocidad constante, continuará haciéndolo a menos que una red distinta de cero fuerza. La segunda ley de Newton nos dice explícitamente cómo cambiará el movimiento como resultado de esta fuerza neta: La aceleración - cambio de velocidad con el tiempo - es directamente proporcional a la fuerza neta. Tenga en cuenta también que tanto la aceleración como la fuerza neta son cantidades vectoriales que apuntan en la misma dirección. TL; DR (demasiado largo; no se leyó) Una fuerza neta de cero NO necesariamente significa que el objeto está detenido! Una fuerza neta de cero tampoco significa que no existan fuerzas que actúen sobre un objeto, ya que es posible que múltiples fuerzas actúen de tal manera que se cancelen entre sí. El primer paso para encontrar la fuerza neta sobre cualquier objeto es dibujar un diagrama de cuerpo libre Por ejemplo, supongamos que un libro está sentado en una mesa. Las fuerzas que actúan sobre él serían la fuerza de gravedad sobre el libro, que actúa hacia abajo, y la fuerza normal de la mesa sobre el libro, que actúa hacia arriba. El diagrama de cuerpo libre de este escenario consistiría en dos flechas de igual longitud que se originan en el centro del libro, una apuntando hacia arriba y la otra apuntando hacia abajo. (imagen 1) Suponga el mismo libro estaba siendo empujado hacia la derecha con una fuerza de 5 N mientras que una fuerza de fricción de 3 N se oponía al movimiento. Ahora el diagrama de cuerpo libre incluiría una flecha de 5 N a la derecha y una flecha de 3 N a la izquierda. (imagen 2) Finalmente, suponga que el mismo libro estaba en una pendiente, deslizándose hacia abajo. En este escenario, las tres fuerzas son la fuerza gravitacional en el libro, que apunta hacia abajo; la fuerza normal sobre el libro, que apunta perpendicular a la superficie; y la fuerza de fricción, que apunta en dirección opuesta a la dirección del movimiento. (imagen 3) Una vez que haya dibujado el diagrama de cuerpo libre, puede usar la suma vectorial para encontrar la fuerza neta que actúa sobre el objeto. Consideraremos tres casos a medida que exploremos esta idea: Caso 1: Todas las fuerzas se encuentran en la misma línea. Si todas las fuerzas se encuentran en la misma línea (apuntando hacia la izquierda y la derecha solamente , o solo hacia arriba y hacia abajo, por ejemplo), determinar la fuerza neta es tan sencillo como sumar las magnitudes de las fuerzas en la dirección positiva y restar las magnitudes de las fuerzas en la dirección negativa. (Si dos fuerzas son iguales y opuestas, como es el caso del libro que descansa sobre la mesa, la fuerza neta \u003d 0) Ejemplo: Considere una bola de 1 kg que cae debido a la gravedad, experimentando una resistencia al aire fuerza de 5 N. Hay una fuerza hacia abajo debido a la gravedad de 1 kg × 9.8 m /s 2 \u003d 9.8 N, y una fuerza hacia arriba de 5 N. Si usamos la convención de que arriba es positivo, entonces la fuerza neta es 5 N - 9.8 N \u003d -4.8 N, lo que indica una fuerza neta de 4.8 N en la dirección hacia abajo. (imagen 4) Caso 2: Todas las fuerzas se encuentran en perpendicular ejes y sumar a 0 a lo largo de un eje. En este caso, debido a las fuerzas que se suman a 0 en una dirección, solo necesitamos enfocarnos en la dirección perpendicular al determinar la fuerza neta. (Aunque el conocimiento de que las fuerzas en la primera dirección se suman a 0 a veces puede darnos información sobre las fuerzas en la dirección perpendicular, como al determinar las fuerzas de fricción en términos de la magnitud de la fuerza normal). Ejemplo: A El coche de juguete de 0.25 kg se empuja por el piso con una fuerza de 3 N que actúa hacia la derecha. Una fuerza de fricción 2-N actúa para oponerse a este movimiento. Tenga en cuenta que la gravedad también actúa hacia abajo en este automóvil con una fuerza de 0.25 kg × 9.8 m /s 2 \u003d 2.45 N, y una fuerza normal actúa hacia arriba, también con 2.45 N. (¿Cómo sabemos esto? Debido a que no hay cambio en el movimiento en la dirección vertical cuando el automóvil es empujado por el piso, por lo tanto, la fuerza neta en la dirección vertical debe ser 0.) (imagen 5) Caso 3: Todas las fuerzas no se limitan a una línea y no se encuentran en ejes perpendiculares. Si sabemos en qué dirección estará la aceleración, elegiremos un sistema de coordenadas donde esa dirección se encuentre en el eje x positivo o en el eje y positivo. A partir de ahí, dividimos cada vector de fuerza en componentes x e y. Como el movimiento en una dirección es constante, la suma de las fuerzas en esa dirección debe ser 0. Las fuerzas en la otra dirección son los únicos contribuyentes a la fuerza neta y este caso se ha reducido al Caso 2. Si no sabemos en qué dirección estará la aceleración, podemos elegir cualquier sistema de coordenadas cartesianas, aunque generalmente es más conveniente elegir uno en el que una o más de las fuerzas se encuentran en un eje. Divide cada vector de fuerza en componentes x e y. Determine la fuerza neta en la dirección x Ejemplo: un automóvil de 0.25 kg rueda sin fricción hacia abajo en una inclinación de 30 grados debido a la gravedad. Usaremos un sistema de coordenadas alineado con la rampa como se muestra. El diagrama de cuerpo libre consiste en la gravedad que actúa directamente hacia abajo y la fuerza normal que actúa perpendicular a la superficie. Debemos dividir la fuerza gravitacional en los componentes x e y, lo que da: Dado que el movimiento en la dirección y (Nota: Esta ecuación nos permite determinar la magnitud de la fuerza normal.) En la dirección x, la única fuerza es F gx Una vez que haya determinado su vector de fuerza neta, encuentre el la aceleración de un objeto es una aplicación simple de la segunda ley de Newton. En el ejemplo anterior del auto de 0.25 kg rodando por el rampa, la fuerza neta era 1.23 N por la rampa, por lo que la aceleración sería:
es la suma vectorial de todas las fuerzas que actúan sobre un cuerpo. (Recuerde que una fuerza es un empuje o un tirón). La unidad SI para la fuerza es el newton (N), donde 1 N \u003d 1 kgm /s 2.
\\ bold {F_ {net}} \u003d \\ bold {F_1 + F_2 + F_3 + ...}
\\ bold {F_ {net}} \u003d m \\ bold {a}
Diagramas de cuerpo libre
(FBD) que muestre todas las fuerzas que actúan sobre ese objeto. Esto se hace representando cada vector de fuerza como una flecha que se origina en el centro del objeto y apuntando en la dirección en que actúa la fuerza.
Cálculo de la fuerza neta
Esto simplifica todo al caso unidimensional porque las únicas fuerzas que no se cancelan están en una sola dirección. La fuerza neta sobre el automóvil es entonces 3 N - 2 N \u003d 1 N a la derecha.
y la fuerza neta en la dirección y
por separado. El resultado proporciona las coordenadas x e y de la fuerza neta.
F_ { gx} \u003d F_g \\ sin (\\ theta) \\\\ F_ {gy} \u003d F_g \\ cos (\\ theta)
es constante, sabemos que la fuerza neta en el y
la dirección debe ser 0:
F_N - F_ {gy} \u003d 0
, por lo tanto:
F_ {net} \u003d F_ {gx} \u003d F_g \\ sin (\\ theta) \u003d mg \\ sin (\\ theta) \u003d 0.25 \\ times9.8 \\ times \\ sin (30) \u003d 1.23 \\ text {N} Cómo encontrar la aceleración de la fuerza neta
\\ bold {F_ {net}} \u003d m \\ bold {a} \\ implica \\ bold {a} \u003d \\ frac {\\ bold {F_ {net}} } {m}
\\ bold {a} \u003d \\ frac {\\ bold {F_ {net}}} {m} \u003d \\ frac {1.23} {0.25 } \u003d 4.92 \\ text {m /s} ^ 2 \\ text {por la rampa}