La rama de las matemáticas conocida como topología se ha convertido en una piedra angular de la física moderna gracias a las notables (y sobre todo fiables) propiedades que puede impartir a un material o sistema. Desafortunadamente, identificar sistemas topológicos, o incluso diseñar otros nuevos, es generalmente un proceso tedioso que requiere hacer coincidir exactamente el sistema físico con un modelo matemático.
Investigadores de la Universidad de Ámsterdam y de la École Normale Supérieure de Lyon han demostrado un método sin modelos para identificar la topología, lo que permite descubrir nuevos materiales topológicos mediante un enfoque puramente experimental. La investigación se publica en la revista Proceedings of the National Academy of Sciences. .
La topología abarca las propiedades de un sistema que no pueden cambiarse mediante ninguna "deformación suave". Como se podrá deducir de esta descripción bastante formal y abstracta, la topología comenzó su vida como una rama de las matemáticas. Sin embargo, durante las últimas décadas los físicos han demostrado que las matemáticas subyacentes a la topología pueden tener consecuencias muy reales. Los efectos topológicos se pueden encontrar en una amplia gama de sistemas físicos, desde electrones individuales hasta corrientes oceánicas a gran escala.
Un ejemplo concreto:en el campo de la materia cuántica, la topología saltó a la fama gracias a los llamados aislantes topológicos. Estos materiales no conducen electricidad a través de su masa, pero los electrones se mueven libremente a lo largo de sus superficies o bordes. Esta conducción superficial persistirá, sin obstáculos por las imperfecciones del material, siempre y cuando no se haga algo drástico como cambiar toda la estructura atómica del material.
Además, las corrientes en las superficies o bordes de un aislante topológico tienen una dirección establecida (dependiendo del espín del electrón), impuesta nuevamente por la naturaleza topológica de la estructura electrónica.
Estas características topológicas pueden tener aplicaciones muy útiles y la topología se ha convertido en una de las fronteras de la ciencia de los materiales. Además de identificar materiales topológicos en la naturaleza, los esfuerzos de investigación paralelos se centran en el diseño de materiales topológicos sintéticos desde abajo hacia arriba.
Los estados de borde topológicos de estructuras mecánicas conocidas como "metamateriales" presentan oportunidades inigualables para lograr respuestas confiables en guía de ondas, detección, computación y filtrado.
La investigación en esta área se ve frenada por la falta de métodos experimentales para investigar la naturaleza topológica de un sistema. La necesidad de hacer coincidir un modelo matemático con un sistema físico limita la investigación a materiales para los que ya tenemos una descripción teórica y constituye un cuello de botella para identificar y diseñar materiales topológicos.
Para abordar este problema, Xiaofei Guo y Corentin Coulais del Laboratorio de Materiales de Máquinas de la Universidad de Ámsterdam se asociaron con Marcelo Guzmán, David Carpentier y Denis Bartolo de ENS Lyon.
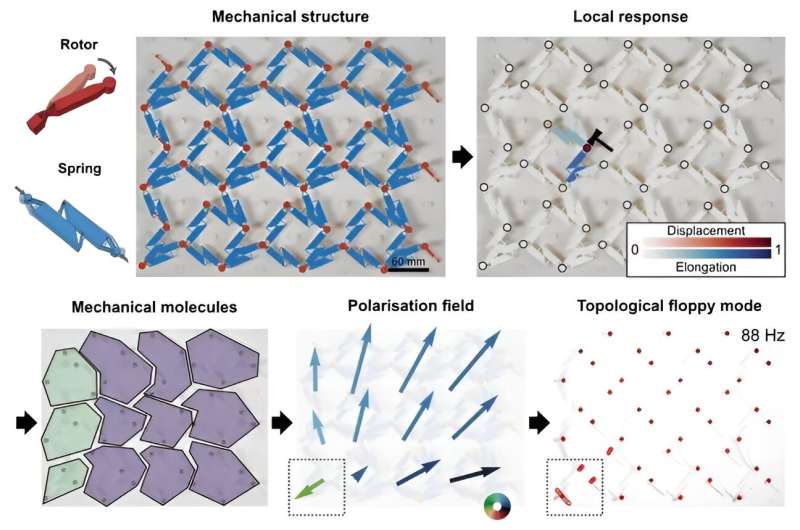
"Hasta ahora, la mayoría de los experimentos tenían como objetivo probar teorías o mostrar predicciones teóricas en revistas", dice Guo. "Encontramos una manera de medir puntos blandos o frágiles topológicamente protegidos en metamateriales mecánicos desconocidos sin necesidad de modelado. Nuestro enfoque permite la exploración práctica y la caracterización de las propiedades de los materiales sin profundizar en marcos teóricos complejos".
Los investigadores demostraron su método con metamateriales mecánicos que consisten en una red de rotores (varillas rígidas que pueden girar) conectados por resortes elásticos. La topología en estos sistemas puede hacer que algunas regiones de dicho metamaterial sean particularmente flexibles o rígidas.
Bartolo afirma:"Nos dimos cuenta de que sondear selectivamente un material localmente podría brindarnos toda la información necesaria para revelar puntos blandos o frágiles en la estructura, incluso en regiones muy alejadas de nuestras sondas. Utilizando esto, desarrollamos un protocolo muy práctico aplicable a un amplia gama de materiales y metamateriales."
Al pinchar rotores individuales en el metamaterial y rastrear los desplazamientos y alargamientos resultantes en el sistema, los investigadores identificaron diferentes "moléculas mecánicas":grupos de rotores y resortes que se mueven como una sola unidad.
De manera análoga a los sistemas electrostáticos, determinaron una "polarización" efectiva de cada molécula, calculada a partir de los movimientos de las moléculas. Esta polarización cambiará repentinamente de dirección en presencia de una característica topológica, lo que hará que la topología inherente sea fácil de identificar.
Los investigadores aplicaron su método a varios metamateriales mecánicos, algunos de los cuales se sabía por estudios anteriores que eran topológicos, mientras que otros eran estructuras nuevas sin un modelo matemático asociado. Los resultados demuestran que la polarización determinada experimentalmente es muy eficaz para señalar características topológicas.
Este enfoque sin modelos no se limita sólo a los sistemas mecánicos; El mismo método podría aplicarse a estructuras fotónicas o acústicas. Hará que la topología sea accesible a una gama más amplia de físicos e ingenieros, y facilitará la construcción de materiales funcionales que vayan más allá de las demostraciones de laboratorio.
Más información: Marcelo Guzmán et al, Caracterización sin modelos de estados topológicos de bordes y esquinas en redes mecánicas, Actas de la Academia Nacional de Ciencias (2024). DOI:10.1073/pnas.2305287121
Información de la revista: Actas de la Academia Nacional de Ciencias
Proporcionado por la Universidad de Ámsterdam