Un nuevo estudio realizado por científicos de Japón explora la propagación de información cuántica dentro de sistemas de bosones que interactúan como los condensados de Bose-Einstein (BEC), revelando el potencial de una transmisión acelerada a diferencia de lo que se pensaba anteriormente.
Los sistemas cuánticos de muchos cuerpos, como los sistemas de bosones que interactúan, son de fundamental importancia ya que encuentran aplicaciones en diversas ramas de la física. La propagación de información en sistemas cuánticos de muchos cuerpos se rige por el límite de Lieb-Robinson. Esto cuantifica la rapidez con la que la información o los cambios se propagan a través de un sistema cuántico.
Cuando se realiza un cambio en una parte del sistema, el límite de Lieb-Robinson describe la velocidad a la que este cambio influye en otras partes del sistema. En términos prácticos, significa que el efecto de su cambio inicial se extenderá desde su punto de origen, afectando a las regiones vecinas del sistema.
Sin embargo, el vínculo de Lieb-Robinson con los sistemas de bosones en interacción sigue siendo un desafío desde hace mucho tiempo.
Los investigadores, dirigidos por el Dr. Tomotaka Kuwahara, líder del equipo RIKEN Hakubi en el Centro RIKEN de Computación Cuántica, abordan este desafío en su nuevo Nature Communications. estudio.
El Dr. Kuwahara explicó la importancia de su trabajo a Phys.org, destacando la importancia de comprender los sistemas cuánticos que contienen partículas fundamentales como bosones y fermiones.
"Los sistemas de bosones, en principio, no tienen límite de energía, lo que hizo que la unión de Lieb-Robinson a sistemas bosónicos fuera un desafío significativo", afirmó.
Como se mencionó anteriormente, el límite de Lieb-Robinson proporciona un límite cuantitativo sobre la rapidez con la que las correlaciones o influencias pueden extenderse entre regiones espacialmente separadas de un sistema cuántico.
Esto significa que la propagación no puede realizarse instantáneamente en todas partes, sino que se limita a un cono de luz efectivo. Inspirado en la teoría de la relatividad de Einstein, el cono de luz representa todos los puntos en el espacio y el tiempo a los que puede llegar una señal luminosa emitida por un evento. Esto crea un doble cono:uno para el pasado y otro para el futuro.
Lo mismo se aplica a la propagación de información en sistemas cuánticos de muchos cuerpos, es decir, sistemas con más de dos partículas cuánticas.
"El límite de Lieb-Robinson establece un límite de velocidad universal para la velocidad con la que la información puede viajar en estos sistemas", explicó el Dr. Kuwahara.
Según el límite de Lieb-Robinson, la propagación de información es limitada y decae exponencialmente con la distancia o el tiempo. Los detalles de la decadencia dependen del sistema individual y de las interacciones que pueden ocurrir dentro del sistema.
Formulado por Elliott Lieb y Derek Robinson en 1972, el límite de Lieb-Robinson sólo es aplicable a sistemas no relativistas, es decir, que la información viaja a velocidades mucho menores que la velocidad de la luz.
Los sistemas de bosones que interactúan constan de muchos bosones (como fotones). Estos sistemas, si bien son comunes, presentan muchos desafíos, como interacciones de largo alcance entre bosones y energía ilimitada, lo que dificulta el desarrollo de simulaciones y modelos teóricos.
Pero, desde el descubrimiento del BEC, se han desarrollado modelos como el modelo de Bose-Hubbard para estudiar sistemas bosónicos. El modelo de Bose-Hubbard es un marco teórico utilizado para comprender cómo se comportan los bosones cuando están confinados en una estructura reticular, como los átomos en un cristal.
Este modelo tiene en cuenta dos factores principales. El primero es el salto de bosones de un sitio de la red a otro, representado por el parámetro de salto. El segundo es el parámetro de interacción en el sitio, que representa las fuerzas repulsivas entre bosones cuando ocupan el mismo sitio. Esta energía de interacción aumenta a medida que más bosones ocupan el mismo sitio.
Estos factores incorporan la interacción entre los bosones, razón por la cual los investigadores eligieron el modelo de Bose-Hubbard para investigar los límites de Lieb-Robinson en sistemas de bosones que interactúan.
Los investigadores optaron por estudiar el límite de Lieb-Robinson para una red dimensional D (sistema de bosones interactivos) gobernada por el modelo de Bose-Hubbard. Encontraron tres resultados para este sistema.
Este resultado aborda la interacción de bosones dentro de la red. Los investigadores descubrieron que la velocidad del transporte de bosones es limitada, incluso en sistemas con interacciones de largo alcance. Esta velocidad, aunque limitada, crece como máximo de forma logarítmica con el tiempo, lo cual es relativamente lento.
Este hallazgo proporciona información crucial sobre la dinámica de los sistemas de bosones, poniendo un límite superior a su velocidad.
Este resultado se centra en la propagación de los operadores del sistema a lo largo del tiempo. Los operadores son básicamente variables del sistema, como el impulso. A medida que estos operadores se propagan, se desvían de la evolución ideal, lo que lleva a la acumulación de errores.
Esta propagación de errores determina qué tan rápido se puede propagar la información en el sistema. Por ejemplo, si el error es grande, indica que la propagación de la información es más lenta o más restringida, ya que la aproximación se desvía significativamente de la evolución ideal del sistema.
De manera similar, si el error es pequeño, entonces la propagación de la información es rápida. Esto se alinea con el límite de Lieb-Robinson, lo que indica la presencia de un límite superior en la propagación de errores.
A pesar de la presencia de un límite superior en la propagación de errores, las interacciones entre bosones inducen agrupaciones en regiones específicas. Estas regiones, caracterizadas por concentraciones más altas de bosones, facilitan la propagación acelerada de información a lo largo de ciertas rutas o direcciones de la red.
Este fenómeno se alinea con el límite de Lieb-Robinson. Sin embargo, esta aceleración es acotada y tiene un crecimiento polinómico dependiendo de la dimensionalidad del sistema.
Este resultado presenta una forma de simular estos sistemas utilizando puertas cuánticas elementales (como CNOT). Los investigadores proporcionan un límite superior para el número de puertas cuánticas elementales necesarias para simular eficientemente la evolución temporal de los sistemas de bosones que interactúan.
Los sistemas fermiónicos muestran un límite de velocidad finito para la rapidez con la que se puede propagar la información. Antes de este trabajo, los científicos asumían lo mismo para los sistemas bosónicos, lo cual no es cierto.
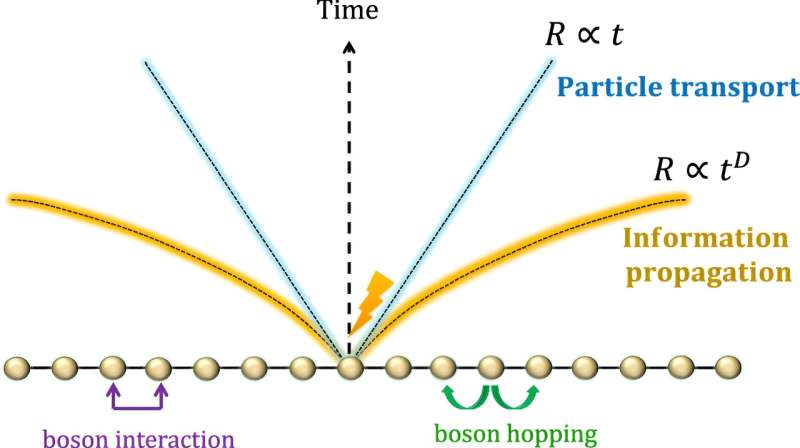
"El cono de luz se propaga mucho más rápido y no es lineal, es decir, se acelera con el tiempo. Específicamente, si miras un espacio tridimensional, la distancia que la 'información' puede recorrer crece con el cuadrado del tiempo. Entonces, en este sentido, los bosones pueden enviar información mucho más rápido que los fermiones, especialmente a medida que pasa el tiempo", explicó el Dr. Kuwahara.
Esto depende de la cantidad de bosones que pueden ocupar el mismo estado al mismo tiempo. Esencialmente, cuantos más bosones se unan, más rápido se podrá propagar la información.
"Pero, dado que los bosones sólo pueden moverse con una velocidad finita, muchos de ellos necesitan un poco de tiempo para reunirse, lo que lleva a una velocidad limitada de propagación de la información. Con el tiempo, a medida que más bosones cooperan, la velocidad a la que se mueven puede enviar información aumenta", dijo el Dr. Kuwahara.
Este trabajo abre una nueva ventana a la exploración de sistemas de bosones que interactúan para la propagación de información.
"Anticipo que el algoritmo se utilizará para simular la física de la materia condensada, lo que podría conducir al descubrimiento de nuevas fases cuánticas. También debería resultar útil para simular la termalización cuántica, ayudando a abordar la cuestión básica de cómo los sistemas cuánticos cerrados se asientan en una estado estable a lo largo del tiempo", concluyó el Dr. Kuwahara.
Más información: Tomotaka Kuwahara et al, Cono de luz eficaz y simulación cuántica digital de bosones que interactúan, Nature Communications (2024). DOI:10.1038/s41467-024-46501-7.
Información de la revista: Comunicaciones sobre la naturaleza
© 2024 Red Ciencia X