Agregar una regla simple a un juego de billar idealizado conduce a una gran cantidad de preguntas matemáticas intrigantes, así como a aplicaciones en la física de los organismos vivos. Esta semana, investigadores de la Universidad de Ámsterdam, incluidos dos estudiantes de maestría como primeros autores, publicaron un artículo en Physical Review Letters. sobre la fascinante dinámica del billar con memoria.
Una versión idealizada del juego de billar ha fascinado a los matemáticos durante décadas. La pregunta básica es sencilla:una vez que se juega una bola de billar, ¿adónde va y dónde termina? Supongamos que el billar es perfecto:las paredes rebotan perfectamente, no hay otros objetos sobre la mesa, el movimiento de la bola no tiene fricción, etc. Entonces la pelota realmente no "terminará" en ninguna parte; continuará para siempre.
¿Pero alguna vez regresa al punto donde comenzó? ¿Al final visita cada parte de la mesa? Cuando cambiamos ligeramente la dirección de la bola, o su ubicación inicial, ¿el camino que sigue se parece al anterior?
Todas estas preguntas resultan muy intrigantes desde un punto de vista matemático. No siempre se conocen sus respuestas, especialmente cuando la forma del billar no es simple, como un cuadrado o un rectángulo. Por ejemplo, en los billares triangulares con esquinas de menos de 100 grados, se sabe que siempre hay caminos periódicos:caminos que la bola puede seguir y que regresan sobre sí mismos.
Esto se puede demostrar matemáticamente. Ahora, cambia una de las esquinas a un ángulo ligeramente mayor y ningún matemático sabrá la respuesta.
Los juegos de billar idealizados no son sólo el pasatiempo favorito de los matemáticos. También tienen un profundo impacto en la física y otras ciencias. Muchas de las preguntas sobre el billar pueden formularse como preguntas sobre el caos:¿Condiciones iniciales similares de un sistema dinámico (ya sea una bola en una mesa de billar, una molécula en un gas o un pájaro en una bandada) siempre conducen a resultados finales similares? ¿Resultados?
En una investigación realizada en la Universidad de Ámsterdam, un equipo de físicos ha descubierto que cambiando ligeramente las reglas del juego de billar, el número de aplicaciones en el mundo real aumenta aún más.
Mazi Jalaal, coautor de la publicación y jefe del grupo en el que se realizó la investigación, explica:"En la naturaleza, muchos organismos vivos tienen una forma externa de memoria. Por ejemplo, dejan huellas para recordar dónde han estado. Luego pueden usar esa información para seguir la misma ruta nuevamente o, por ejemplo, cuando buscan comida, para no explorar esa misma región nuevamente".
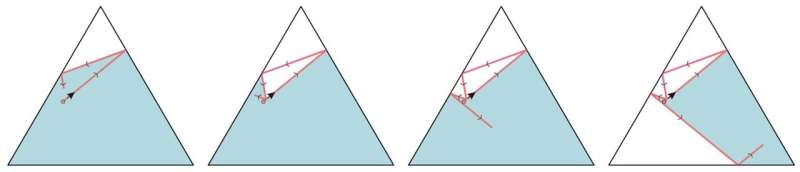
Esta última opción llevó a los investigadores a una idea interesante:¿Qué pasaría si añadimos una regla al juego de billar, es decir, que la bola nunca puede cruzar su camino anterior? El resultado es que el tamaño efectivo de la mesa de billar se hace cada vez más pequeño. De hecho, la pelota eventualmente queda atrapada por su propia trayectoria.
Nuevas preguntas interesantes
El efecto de captura hace que el sistema sea aún más intrigante. Incluso las preguntas más sencillas se vuelven ahora extremadamente fascinantes. ¿Qué distancia recorre una pelota antes de quedar atrapada? La respuesta varía, tanto en la forma de la mesa como en el punto de partida y dirección de la bola.
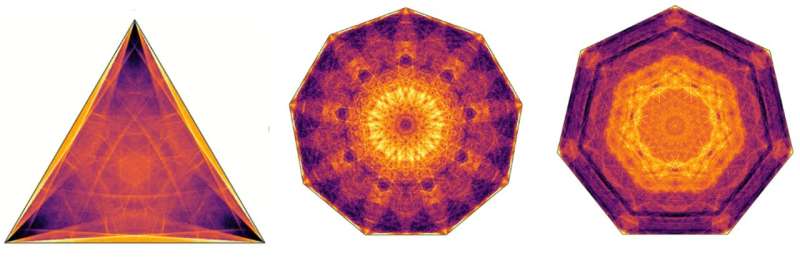
A veces, la pelota recorre una longitud que es solo unas pocas veces el tamaño de la mesa, a veces puede recorrer 100 veces esa longitud antes de quedar atrapada. Dónde termina finalmente la pelota en su estado atrapado también es una cuestión compleja; repetir el experimento en una computadora millones de veces, cada vez con una posición inicial y una velocidad ligeramente diferentes, conduce a hermosos patrones de configuraciones finales.
La imagen en la parte superior de este texto muestra algunos de estos hermosos ejemplos. Curiosamente, los sistemas dinámicos resultantes pueden ser caóticos. Cambiar solo ligeramente la posición inicial o la velocidad de la bola que se esquiva puede hacer que quede atrapada en un punto completamente diferente del billar.
Además, al contrario de lo que sucede en una mesa de billar normal, la bola que se esquiva no tiene las mismas probabilidades de terminar en cualquier lugar. Algunas regiones tienen más probabilidades que otras. Para explicar y demostrar todas estas características, los matemáticos ciertamente tienen mucho trabajo por delante.
Una particularidad interesante de la publicación es que sus dos primeros autores son estudiantes de maestría. Jalaal añade:"La idea de un 'billar con memoria' es lo suficientemente simple y nueva como para que estudiarlo no requiera años de experiencia. Thijs y Stijn hicieron un gran trabajo al hacer suyo el material y al encontrar formas inteligentes de estudiar todos estos nuevos problemas abiertos. Estoy muy feliz de que ya puedan ser autores principales de una publicación."
Los resultados son sólo los primeros pasos en lo que podría ser un área de investigación completamente nueva. No sólo hay muchas preguntas matemáticas interesantes que ahora esperan ser respondidas; las aplicaciones en física, incluida la biofísica, también son infinitas.
Jalaal dice:"El concepto de captura es uno que pide ser explorado, también en sistemas de la vida real. Por ejemplo, sabemos que los mohos unicelulares utilizan caminos que los evitan a sí mismos. ¿También quedan atrapados y qué sucede cuando ¿Lo hacen? ¿O tienen mecanismos inteligentes para evitar que esto suceda? ¿Lo utilizan para mejorar las estrategias de búsqueda de alimentos?
"Los resultados nos ayudarían a comprender mejor estos sistemas biológicos y tal vez incluso incorporar las lecciones que aprendemos para optimizar esta forma de billar con memoria para su uso en robots".
Más información: Thijs Albers et al, Billar con memoria espacial, Cartas de revisión física (2024). DOI:10.1103/PhysRevLett.132.157101. En arXiv :DOI:10.48550/arxiv.2307.01734
Información de la revista: Cartas de revisión física , arXiv
Proporcionado por la Universidad de Ámsterdam