Un par de investigadores de la Universit´e Paris-Saclay, CNRS y la Univ Rennes, CNRS, IPR, respectivamente, han usado las matemáticas para ayudar a describir el proceso involucrado cuando las hebras cortas de fibra se retuercen en largos tramos de hilo. En su artículo publicado en la revista Physical Review Letters, Antoine Seguin y Jérôme Crassous describen cómo usaron experimentos y simulaciones para comprender mejor los factores que intervienen cuando las fibras se retuercen entre sí.

Los seres humanos han estado retorciendo hebras cortas de fibras para crear hebras largas de cuerda o hilo durante miles de años, y aunque el proceso general se comprende bien, las matemáticas detrás de él han sido bastante incompletas. En este nuevo esfuerzo, Seguin y Crassous han abordado el problema utilizando un nuevo enfoque, aplicando tanto experimentos como simulaciones.

A medida que varias fibras cortas se retuercen juntas, se entrelazan, pero eso, por supuesto, no es suficiente para mantenerlas juntas. Se mantienen unidos debido a la fricción involucrada. Al tirar de los extremos de un trozo de hilo, las hebras individuales de las que está hecho se empujan entre sí, lo que aumenta la cantidad de fricción y, por lo tanto, su resistencia. Pero, ¿existen reglas matemáticas que rijan el proceso? ¿Cuál es el número óptimo de fibras, por ejemplo, para garantizar el hilo más resistente? ¿O qué grado de resistencia le da al hilo el grado de fricción entre dos hebras de fibra?

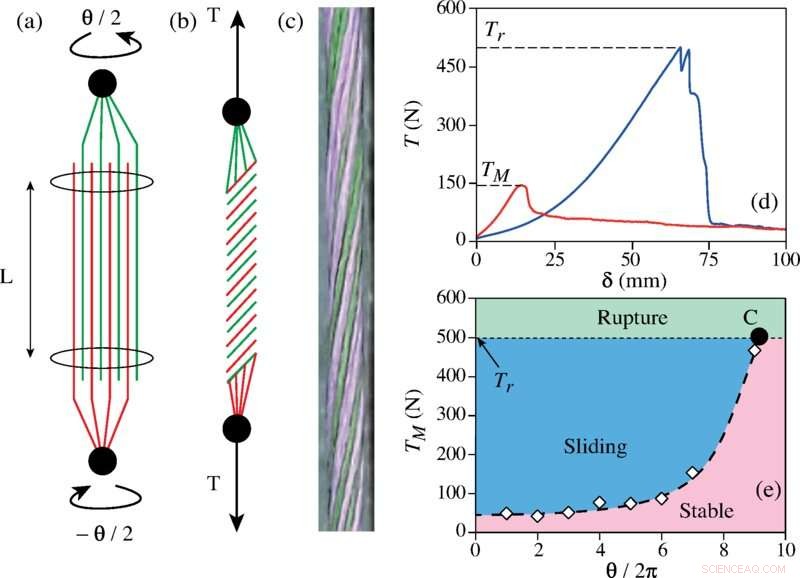
Para encontrar estas respuestas, los investigadores realizaron múltiples pruebas en diferentes fibras retorcidas en hilos. Descubrieron que un aumento en las torsiones aumentaba la fuerza de unión de las fibras, pero solo hasta cierto punto. Además, cada tipo de fibra tenía su propio punto de ruptura. Al crear simulaciones para probar más fácilmente diferentes configuraciones, también encontraron que había un radio de fibra óptimo para una determinada longitud de hilo y que la fuerza del hilo escalaba con el exponencial del cuadrado del ángulo de torsión.

Al buscar puntos en común, descubrieron lo que describen como el número de torsión de Hércules, un parámetro que describe las fuerzas involucradas con el ángulo de torsión, un coeficiente de fricción y el radio del hilo. También encontraron que este número en general era proporcional al cuadrado del número de torsiones aplicadas y tenía un valor crítico de 30. También desarrollaron una fórmula para mostrar el tamaño de radio óptimo para un tipo de fibra determinado. + Explora más

Los investigadores investigan 'por qué la ropa no se deshace'

© 2022 Red Ciencia X