
Esta es una instantánea tomada de una simulación numérica del modelo bidimensional de Wilson-Cowan con entrada estocástica (ecuación (3) en nuestro artículo). Los píxeles amarillos (azules) representan actividad alta (baja). Crédito:Tiberi et al.
Investigaciones anteriores en neurociencia sugieren que las redes neuronales biológicas en el cerebro podrían autoorganizarse en un estado crítico. En física, un estado crítico es esencialmente un punto que marca la transición entre las fases ordenadas y desordenadas de la materia.
Investigadores del Centro de Investigación Jülich, la Universidad RWTH de Aquisgrán y la Universidad de la Sorbona han presentado recientemente una teoría que podría ayudar a explicar la criticidad del cerebro. Esta teoría, presentada en un artículo publicado en Physical Review Letters , se basa en una teoría prototípica del campo neural, conocida como la "ecuación estocástica de Wilson-Cowan".
"Trabajos anteriores han proporcionado evidencia de que el cerebro opera en un punto crítico", dijeron a Phys.org, vía correo electrónico, Lorenzo Tiberi, Jonas Stapmanns, Tobias Kühn, Thomas Luu, David Dahmen y Moritz Helias, los investigadores que llevaron a cabo el estudio. . "Sin embargo, no está claro cuál de los muchos tipos posibles de criticidad es implementado específicamente por el cerebro y cómo este último puede explotar la criticidad para un cálculo óptimo".
Para clasificar los diferentes tipos de criticidad, los físicos suelen utilizar métodos dentro del llamado grupo de renormalización (RG). Estos son enfoques esencialmente formales que se pueden utilizar para investigar sistemáticamente los cambios en un sistema físico a diferentes escalas.
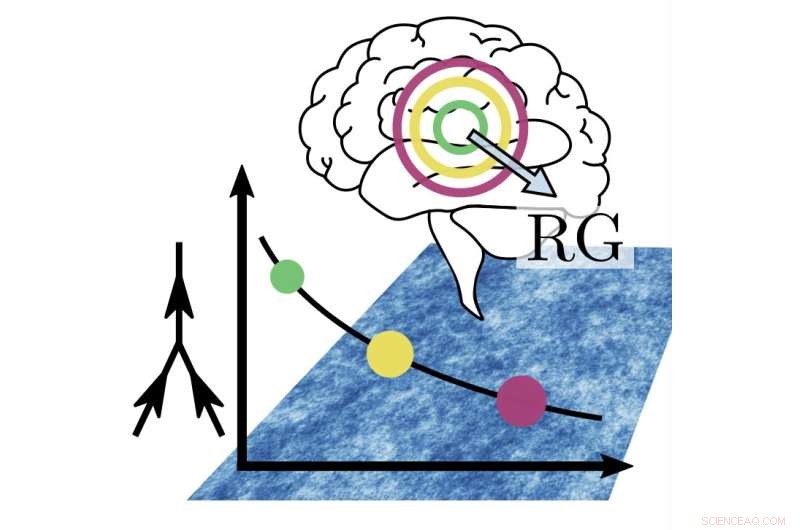
Figura abstracta que ilustra el enfoque del grupo de renormalización (RG). Al observar el sistema en escalas de longitud cada vez más gruesas (indicadas por los círculos concéntricos y la flecha frente al cerebro), la fuerza de las interacciones no lineales (representadas por el diagrama de Feynman a la izquierda) disminuye lentamente y, en particular, permanece distinta de cero incluso en grandes escalas espaciales (curva con puntos de colores). Fondo:igual que la figura 1 pero diferente esquema de color. Crédito:Tiberi et al.
En su estudio, los investigadores adaptaron estos métodos tradicionales y los integraron con un modelo de campo neuronal prototípico propuesto por primera vez por Wilson y Cowan. Luego los aplicaron específicamente al campo de la neurociencia para examinar la criticidad en las redes neuronales biológicas.
"En nuestro trabajo, estudiamos las bien establecidas ecuaciones de Wilson-Cowan con entrada estocástica, por lo que el modelo que usamos no es nuevo", dijeron Tiberi, Stapmanns y sus colegas. "Sin embargo, usando técnicas de RG, llegamos a un resultado original".
Para completar tareas computacionales, tareas cognitivas que implican cálculos, el cerebro humano necesita poder memorizar los datos de entrada que recibe y luego combinarlos de formas complejas. Esto a su vez le permite procesar la información y resolver el problema computacional.
"Descubrimos que la criticidad en el modelo de campo neural de Wilson-Cowan es del tipo Gell-Mann-Low, que, entre todos los tipos de criticidad, ofrece específicamente un equilibrio óptimo entre memorizar datos de entrada y combinarlos en formas complejas", Tiberi, Stapmanns y sus colegas dijeron.
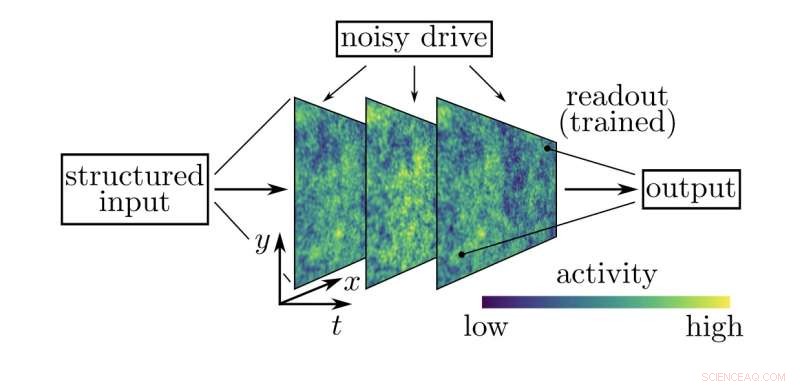
Figura que ilustra la investigación de las capacidades computacionales del modelo. Se agrega un estímulo (entrada estructurada) al sistema (con coordenadas espaciales x e y) que evoluciona a lo largo del tiempo t mientras que la red también es impulsada por una entrada estocástica (impulso ruidoso). Se entrena una lectura lineal para reconstruir o clasificar el estímulo de entrada a partir de una instantánea de la actividad en el sistema. La tarea de reconstrucción prueba la memoria del sistema, mientras que la tarea de clasificación requiere interacciones no lineales. Crédito:Tiberi et al.
Usando métodos RG, los investigadores lograron estudiar los efectos de las interacciones no lineales en el modelo de Wilson-Cowan, que son cruciales para comprender cómo el cerebro procesa la información. Este es un logro notable, ya que los métodos de campo medio utilizados por otros equipos en el pasado no pudieron capturar estos efectos, particularmente cuando las interacciones son lo suficientemente fuertes como para dar forma a la dinámica cerebral en una escala macroscópica.
"Esperamos que los métodos RG sean útiles para estudiar otros procesos no lineales en las redes neuronales", explicó el equipo. "Además, establecemos conexiones con otras áreas de la física:el concepto de criticidad Gell-Man-Low se origina en la teoría cuántica de campos y el modelo Kardar-Parisi-Zhang, que se relaciona estrechamente con nuestro modelo, se utilizó originalmente para describir el crecimiento dinámico. de interfaces."
En el futuro, la teoría presentada por este equipo de investigadores podría usarse para examinar otras dinámicas cerebrales y procesos neuronales, más allá de la criticidad. Además, en última instancia, podría allanar el camino hacia la introducción de otras construcciones teóricas que fusionen la física y la neurociencia.
"En el cerebro, la fuerza de las conexiones entre las neuronas es muy variable hasta el punto de que, en una primera aproximación, puede describirse como aleatoria", agregaron los investigadores. "Ahora planeamos aplicar nuestros métodos a modelos neuronales que incluyen esta función y ver qué efecto tiene esto, si lo hay, en el tipo de criticidad que encontramos".
© 2022 Red Ciencia X Optimización de redes neuronales en una computadora inspirada en el cerebro