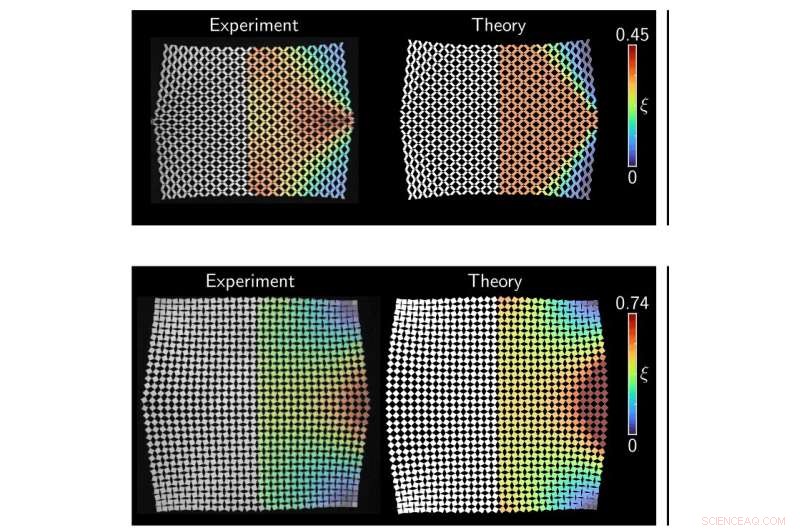
Dos patrones de celdas de 16 × 16 después de la deformación. La fila superior no es auxética (se contrae cuando se tira) e hiperbólica o en forma de onda. La fila inferior es auxética (se expande cuando se tira) y elíptica. Crédito:Paul Plucinsky
Una grulla de papel tradicional es una proeza del arte. Cada pliegue en origami conduce a la transformación de una sola hoja de papel cuadrada en un pájaro, un dragón o una flor. Origami desaconseja pegar, marcar o cortar el papel, pero en el arte del kirigami, los cortes colocados estratégicamente pueden transformar aún más la forma del papel, creando estructuras complejas a partir de simples cortes. Un ejemplo bien conocido de esto es un libro emergente, en el que, dependiendo de cómo se corte el papel plano, emergerá un conjunto diferente de formas (un corazón, una rana, un conjunto de rascacielos) cuando se abra el libro.
En la fabricación, kirigami está cambiando el juego de lo que es posible. Al igual que con el papel, el corte láser repetido de una hoja abre la posibilidad de transformaciones de formas complejas impulsadas por la apertura y cierre de rendijas. Debido a la libertad disponible en el diseño de rendijas, esto crea una amplia variedad de geometrías que tienen propiedades altamente adaptables en comparación con los materiales tradicionales. En aplicaciones del mundo real, es posible que vea un material de este tipo utilizado en robótica o en el espacio, por ejemplo, un material inspirado en la piel de una serpiente como el kirigami que permite que un robot se arrastre o una estructura de avión que se transforma. Pero antes de que estos materiales puedan adaptarse para uso profesional, debemos comprender mejor cómo los materiales de kirigami cambian de forma bajo las tensiones y cargas típicas de la ingeniería. Si bien se conocen las reglas para los bloques de construcción simples, las reglas para sus interacciones colectivas de cambio de forma siguen siendo poco claras.
En un artículo reciente publicado en Physical Review Letters , un equipo interdisciplinario de investigadores de la USC, la Universidad de Illinois en Chicago y la Universidad de Stony Brook derivaron una nueva ecuación matemática para categorizar el comportamiento de los materiales inspirados en kirigami para predecir mejor cómo se moverán cuando se empujen o tiren. El equipo incluye al profesor asistente de la USC Paul Plucinsky y al becario postdoctoral Yue Zheng; el profesor asistente de la Universidad de Stony Brook, Paolo Celli, y el asistente de investigación de posgrado, Imtiar Niloy; y el profesor asistente Ian Tobasco de la Universidad de Illinois-Chicago.
Plucinsky dijo:"La geometría de estos materiales se ajusta de manera un tanto arbitraria. Por lo tanto, necesitamos reglas sobre cómo puede elegir las arquitecturas que va a fabricar. Una vez que tenga esas reglas, también debe poder modelar el sistema para haces una predicción razonable de cómo se deformará cuando lo empujes o lo jales".
Plucinsky dice que los modelos anteriores de comportamiento material no se aplican a los materiales kirigami, ya que no son sensibles a la geometría complicada de sus diseños. "Si desea poder usar estos materiales, primero debe comprender por qué cuando introduce estos patrones en las cargas, producen una respuesta muy poco uniforme".
Cuando se corta un material, produce "celdas" o espacios contenidos que se repiten en un patrón, por ejemplo, paralelogramos, dijo Plucinsky. En el caso de los materiales de kirigami, estas celdas se pueden clasificar para que se comporten de una de dos maneras:como ondas o decayendo a lo largo de arcos elípticos, y esto depende solo de si el patrón se comprime o se expande perpendicularmente a la dirección de extracción. Una ecuación matemática gobierna el comportamiento geométrico de cosas como el flujo de agua, dijo Plucinsky, pero para sólidos como estos, es más difícil de derivar. Una ecuación diferencial parcial (PDE) es lo que Plucinsky y su equipo pudieron desarrollar y establecer como la primera pieza de un rompecabezas más grande necesario para hacer que los materiales de kirigami sean aplicables en la práctica.
Un problema de modelado
En este momento, dice Plucinsky, si bien la gente está ansiosa por usar materiales kirigami para diseñar dispositivos en los campos de la robótica blanda, la biomedicina e incluso la investigación espacial, existe un problema básico de modelado que impide su uso. Plucinsky dijo que no se sabe mucho sobre cómo funcionan los materiales de kirigami en condiciones básicas de carga. "Si no tiene una buena herramienta para modelar los sistemas en cuestión, le resultará difícil investigar el espacio de diseño y hacer predicciones completas sobre los patrones individuales", dijo Plucinsky.
A la luz de eso, Plucinsky y su equipo de investigación pensaron:"¿Existe una ecuación matemática simple que pueda caracterizar estos materiales?" "La ecuación", dijo, "permitiría predecir el comportamiento del sistema de una manera numéricamente eficiente". ."
La clave de la ecuación era darse cuenta de que las células kirigami, aunque tenían componentes básicos complicados, podían conceptualizarse como átomos en una red (un conjunto repetido de átomos en 2D), como en un sólido cristalino convencional, donde las unidades son idénticas y se repiten. . A partir de ahí, fue sencillo derivar una ecuación que logró reflejar los cambios en la estructura física de dicho material cuando se manipula. La ecuación da una idea de los escenarios del mundo real, por ejemplo, cómo podría reaccionar un objeto espacial basado en kirigami si una roca lunar aterriza sobre él.
Piezas de rompecabezas de diseño
Los patrones de kirigami, dijo Plucinsky, son beneficiosos por muchas razones, una de las cuales es que son independientes del material de muchas maneras. "Este tipo de paralelismo es agradable con la fabricación aditiva, en la que ahora básicamente pueden entrar y, en varias escalas, crear patrones cuidadosamente diseñados. El punto es que el patrón importa, así que si diseñas el patrón correctamente, la elección del material que usas no importa". No tiene que importar tanto".
Ver el éxito del modelo matemático en la predicción de materiales inspirados en kirigami abre las puertas para usar dicho modelo para otros materiales, dijo Plucinsky. "Estamos trabajando en la idea de que si tienes algo con un patrón repetitivo, puedes encontrar una ecuación que lo modele con precisión. A partir de ahí, podemos darle la vuelta a esto para que si quieres diseñar una propiedad en particular, puede decir, 'oh, debe presentar un patrón de tipo x' y realizar ingeniería inversa". Origami, kirigami inspiran diseños de metamateriales mecánicos