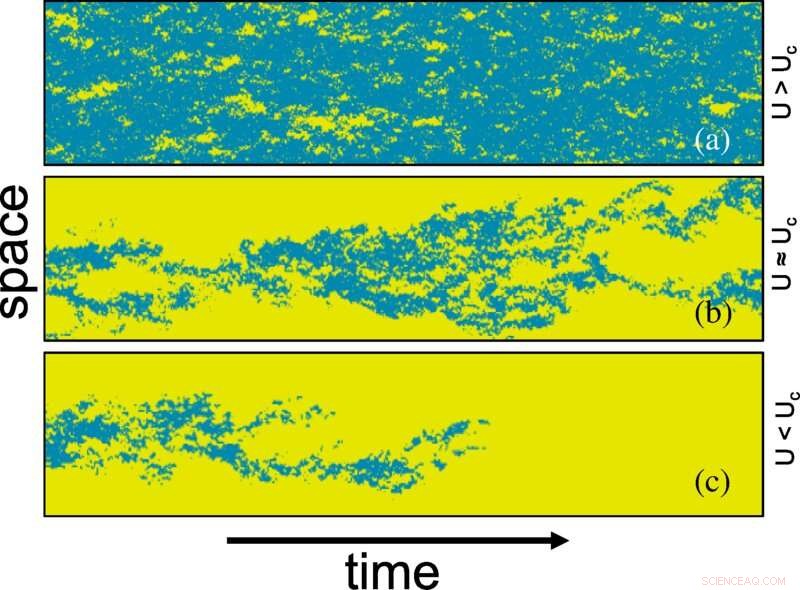
Gráfico de espacio-tiempo de la transición laminar-turbulenta en función de U (es decir, el número de Reynolds) generado por el modelo PP en un flujo cuasi-1D de Taylor-Couette. La turbulencia (en azul) está representada por la densidad de presa B, generada por simulación de Monte Carlo en una red 2D de tamaño 20 × 3000 (a) debajo del punto crítico U=0.0135, (b) en el punto crítico U=0.01425, y (c) por encima del punto crítico U=0.0165. El amarillo representa la fase laminar localmente desocupada por la presa. La densidad de la presa se binariza según sea mayor que 0,065 × la densidad máxima de la presa. Crédito:Cartas de revisión física (2022). DOI:10.1103/PhysRevLett.129.034501
Mencione la palabra "turbulencia" y es posible que evoque imágenes de vuelos accidentados, clima tormentoso y corrientes oceánicas o fluviales agitadas. Para muchos, la turbulencia es un hecho de la vida diaria, pero también es uno de los fenómenos físicos menos comprendidos. En particular, el punto en el que el movimiento de un fluido pasa de un flujo suave y predecible (conocido como "laminar") a aleatorio e impredecible (conocido como "turbulencia"), la llamada transición laminar-turbulenta, continúa desconcertando a los científicos desde Osborne. Reynolds lo estudió por primera vez experimentalmente en tuberías en 1883.
Ahora, un equipo de científicos con sede en la Universidad de Illinois Urbana-Champaign, la Universidad de California en San Diego y la Academia Sínica en Taiwán han demostrado cómo explicar los patrones aleatorios y la dinámica de la turbulencia en las tuberías en el régimen de transición. Su trabajo utiliza ideas novedosas que se originan en campos tan dispares como la mecánica estadística y la ecología y se basa en la creciente evidencia de que la transición laminar-turbulenta tiene propiedades estadísticas que se pueden considerar mejor en términos de la teoría de las transiciones de fase de no equilibrio.
El equipo está compuesto por el estudiante graduado de física de la UIUC, Xueying Wang, el investigador de la Academia Sinica, Hong-Yan Shih, y el presidente emérito de física e investigación de la UIUC Swanlund, Nigel Goldenfeld. Goldenfeld es actualmente Profesor Distinguido de Física de los Cancilleres en la Universidad de California en San Diego.
Los autores publicaron sus resultados el 11 de julio de 2022 en la revista Physical Review Letters .
Puffs y slugs son características de la turbulencia de transición
Reynolds descubrió que en las tuberías, la transición laminar-turbulenta ocurre de manera irregular a medida que aumenta la velocidad del flujo. Las gotas de fluido turbulento, conocidas hoy como "soplos", aparecen cerca de la transición laminar-turbulenta y están separadas por regiones de flujo laminar. Las formas precisas en que las bocanadas aparecen y se mueven o incluso se dividen en dos dependen de la geometría del espacio a través del cual fluye un fluido. Estos fenómenos complejos contribuyen a la merecida reputación de la turbulencia como uno de los últimos problemas pendientes de la física clásica. Incluso a velocidades más altas, los parches turbulentos en realidad crecen en lugar de simplemente moverse o dividirse:estas regiones de turbulencia en crecimiento se denominan "babosas".
Para construir una imagen más clara de la transición a la turbulencia, los investigadores desarrollaron un nuevo modelo mínimo para comprender las bocanadas y las babosas utilizando métodos importados de la biología teórica de la población. Los investigadores descubrieron que podían representar el flujo de energía del fluido cerca de la transición laminar-turbulenta en términos del flujo de energía que surge en un ecosistema depredador-presa, en el que los nutrientes son la energía del flujo de fondo, el depredador es una determinada estructura de flujo. que inhibe la turbulencia, y la turbulencia es la presa. Este modelo ecológico recapitula el comportamiento turbulento tanto en la tubería como en el flujo de Taylor-Couette, un tipo de flujo rotacional, un objetivo que los modelos anteriores no lograron.
Goldenfeld dice:"Hace seis años, se hizo un gran avance con evidencia teórica y experimental que convergieron en una descripción de bocanadas turbulentas que emergen del flujo laminar, en términos de la teoría de transición de fase. Sin embargo, ese trabajo dejó abierta la pregunta de qué sucede a mayor flujo. se aleja del punto de inflexión.
"Nuestro nuevo trabajo muestra que el mismo marco conceptual y métodos también se aplican en el régimen de slug y recapitulan con notable detalle los hallazgos experimentales. Es fantástico ver los conceptos de la teoría de transición de fase y la ecología unirse en el problema completamente diferente de la mecánica de fluidos. "
Las babosas en sí exhiben comportamientos interesantes y vienen en dos sabores, babosas débiles y babosas fuertes, las cuales se caracterizan por al menos un "frente", una región que contiene un límite entre fluidos laminares y turbulentos.
El autor principal, Wang, explica:"El frente de una babosa es como un frente meteorológico. En un lado del frente hay un fluido laminar. En el otro lado hay turbulencia. El frente es como un límite de fase y se mueve en el espacio a un ritmo constante. velocidad. En las tuberías se obtienen tanto slugs como soplos. Pero los slugs débiles a velocidades de fluido más bajas tienen solo un frente aguas arriba, mientras que los slugs fuertes a velocidades más altas tienen frentes tanto en las direcciones aguas arriba como aguas abajo. Estos factores y la riqueza de los fenómenos de transición hacen que entender la turbulencia transicional realmente difícil. Nuestro trabajo proporciona un marco unificado que maneja todos estos regímenes, diferentes geometrías de flujo y la aleatoriedad inherente".
Los modelos depredador-presa y la turbulencia convergen
Los investigadores pudieron aprovechar una conexión sorprendente que habían encontrado en trabajos anteriores entre la biología de la población y la turbulencia de transición.
Modelar cómo los depredadores interactúan con sus presas es un tema popular en la biología de poblaciones. La idea básica es sencilla:los depredadores se reproducen y comen presas, reduciendo su población; las presas también se reproducen, restaurando su número y proporcionando comida a los depredadores. Entonces el ciclo se repite. En pocas palabras, los depredadores inhiben a las presas, mientras que las presas refuerzan a los depredadores. Los científicos pueden deducir mucha información de estos modelos, como la forma en que las poblaciones de depredadores y presas varían con el tiempo, así como el tiempo que tarda cada uno en desaparecer debido, por ejemplo, a la falta de alimentos o a la depredación excesiva.
En un estudio anterior, Shih y Goldenfeld, trabajando con el ex estudiante universitario Tsung-Lin Hsieh (ahora becario postdoctoral en la Universidad de Princeton), demostraron que existe una analogía entre los modelos depredador-presa y la turbulencia que se puede expresar en términos matemáticos. Cuando el fluido fluye a través de una tubería, se generan dos tipos de movimiento de fluido. El primer tipo es un patrón de vórtice que se arremolina alrededor del eje de la tubería, llamado "flujo zonal". El segundo tipo es la turbulencia a lo largo del eje de la tubería. Los autores encontraron que la turbulencia se acumula constantemente y activa el flujo zonal, que posteriormente suprime la turbulencia. En otras palabras, el flujo zonal corresponde a los depredadores y la turbulencia corresponde a las presas.
Los investigadores encontraron que la distribución de probabilidad del tiempo de vida de la turbulencia transicional coincidía con precisión con la de los depredadores y las presas en un ecosistema, una conexión sorprendente considerando que la biología de la población y la dinámica de fluidos son campos aparentemente dispares.
Hong-Yan Shih comments, "This connection helps us understand the complex transitional behavior of turbulence from the point of view of phase transitions in statistical mechanics. Specifically, this discovery provides the key ingredients to construct an effective theory, which leads to the prediction that the laminar-turbulent transition in fluids is a non-equilibrium phase transition in the directed percolation universality class.
"Directed percolation can be thought of as the familiar process that happens when water drips through coffee grounds in a percolator. If the grounds are too tightly packed, water can't get through. On the other hand, if the grounds are too loosely packed, water can get through but the coffee is undrinkable. There's a critical point where the water just manages to get through and takes long enough so that the coffee tastes good.
"Mathematically, that phenomenon is exactly what happens in the transition to turbulence and the transition of a functioning ecosystem. The mathematics of phase transitions, founded in the Nobel Prize–winning work of K. Wilson, explains how this remarkable phenomenon arises."
This prior work, however, looked at the turbulence of a single puff. Real life isn't as simple, and real fluids near the laminar-turbulent transition contain multiple puffs that grow, die out, and interact in complex ways as the flow speed increases. The researchers needed to extend their model to capture more complicated dynamics beyond those of a single puff.
Extending the predator-prey model by incorporating nutrients
To capture the complex dynamics found in experiments beyond the critical point in the current study, the authors decided to take into account energy balance in pipe flow.
Wang explains, "Turbulence is a dissipative structure that needs constant energy input to be sustained, and that energy comes from the laminar flow. This fact was previously shown by exact computer simulations of the fluid equations, but did not allow us to understand in a predictive way the phenomena that would emerge."
The researchers realized that, just like zonal flow and turbulence require energy to persist, predators and prey need nutrients from their environment to survive.
"We wanted to make a minimal model of the full energy balance to extend the previous work and capture energy extraction of turbulence from laminar mean flow," Wang adds. "So we introduced another component into the 'ecosystem':nutrients, which represent the kinetic energy of the mean flow."
The researchers numerically simulated the extended predator-prey model on a two-dimensional lattice having a length much larger than its width. They watched what happens when nutrients—that is, laminar state energy, from the fluid dynamics perspective—flow into the ecosystem, are consumed by the turbulence, and are restored downstream of the turbulence.
The model maps several pathways for energy and population dynamics. The first pathway takes input energy from the energy budget to turbulent energy, like prey extracting nutrients from their environment. A second pathway takes turbulent energy to zonal flow energy, like predators eating prey.
Once they established these predator-prey-inspired pathways, they sat back and watched computer simulations based on the new model, wherein energy entered the pipe and passed through the pathways randomly. Out of the randomness emerged features of transitional turbulence such as puffs, slugs, and their associated fronts, reproducing results seen in experiments. The simulations showed that the appearance of puffs or slugs—and whether slugs are of the weak or strong type—is determined by the input energy (or equivalently, the speed) of the fluid flow.
The researchers then successfully reproduced all the transitional phenomena observed in pipe flow experiments and explained the underlying physics of puff splitting and growth. Specifically, they found that puff splitting and interaction is highly probabilistic. As the fluid speed increases, the probability of puff splitting also increases. The puff-slug transition is gradual, and it occurs when puffs split so frequently that they start to fill up the system densely.
Rotational flow and new questions for turbulence
In addition to pipe flow, the researchers also simulated a special type of rotational flow known as Taylor-Couette flow in which a fluid moves in the space between two concentric cylinders and the outer cylinder rotates relative to the inner one. Unlike pipe flow, where the energy enters from the high-pressure end of the pipe, Taylor-Couette flow is sustained by shear, the stress that occurs when two boundaries move parallel to one another. The new model easily incorporated this difference and reproduced the patterns of transitional turbulence seen in experiments, demonstrating the flexibility of the model.
"We showed that the rich and complicated dynamical features in transitional pipe flow can be understood with a simple three-level stochastic predator-prey model based on energy balance in pipe flow," says Wang. "Our model also works for quasi-one-dimensional Taylor-Couette flow. Since energy balance generally holds in fluid systems, we expect our model to be applicable to systems with more complicated geometries as well."
Having described turbulence broadly by implementing their model in two different geometries, the team is already looking to answer new questions.
Goldenfeld says, "The next challenge is to see if and how our probabilistic model can be extended to two- or three-dimensional flows. This problem has been intensely studied for well over twenty years, with new experimental data starting to appear."
For his part, Goldenfeld is pleased to see diverse techniques converge to solve problems in complementary ways, a beautiful demonstration of how different fields of science can inform each other.
Goldenfeld summarizes, "Our results show how stochastic dynamics, pattern formation, phase transitions, and modeling concepts from diverse fields such as ecology can bring new tools, predictions, and insights into a problem previously considered within the more narrow disciplinary focus of fluid dynamics. It is exciting to see how successful minimal modeling is at capturing complex physical phenomena in a quantitative way." Ecological extinction explains how turbulence dies