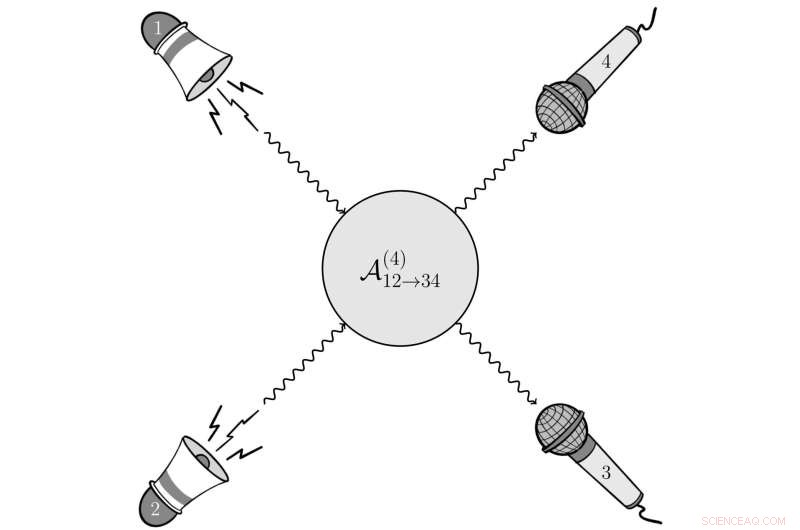
Se producen dos ondas sonoras (1 y 2), que se dispersan en otras dos ondas sonoras (3 y 4), que luego se detectan. La probabilidad de este proceso se describe mediante una amplitud de dispersión de 4 puntos. Crédito:Angelo Esposito
No todo necesita ser visto para ser creído; ciertas cosas se escuchan más fácilmente, como un tren que se acerca a su estación. En un artículo reciente, publicado en Physical Review Letters , los investigadores han puesto sus oídos en el riel, descubriendo una nueva propiedad de amplitudes de dispersión basadas en su estudio de ondas de sonido a través de materia sólida.
Ya sea luz o sonido, los físicos consideran la probabilidad de interacciones de partículas (sí, el sonido puede comportarse como una partícula) en términos de curvas de probabilidad o amplitudes de dispersión. Es un saber común que cuando el impulso o la energía de una de las partículas dispersadas llega a cero, las amplitudes de dispersión siempre deben escalar con potencias enteras del impulso (es decir, p 1 , p 2 , p 3 , etc.). Sin embargo, lo que encontró el equipo de investigación fue que la amplitud puede ser proporcional a una potencia fraccionaria (es decir, p 1/2 , p 1/3 , p 1/4 , etc.).
¿Por qué importa esto? Si bien las teorías cuánticas de campos, como el modelo estándar, permiten a los investigadores hacer predicciones sobre las interacciones de partículas con extrema precisión, todavía es posible mejorar los fundamentos actuales de la física fundamental. Cuando se demuestra un nuevo comportamiento, como la escala de potencia fraccionaria, los científicos tienen la oportunidad de revisar o revisar las teorías existentes.
Este trabajo, realizado por Angelo Esposito (Instituto de Estudios Avanzados), Tomáš Brauner (Universidad de Stavanger) y Riccardo Penco (Universidad Carnegie Mellon), considera específicamente las interacciones de las ondas sonoras en los sólidos. Para visualizar este concepto, imagine un bloque de madera con altavoces colocados en ambos extremos. Una vez que se encienden los parlantes, dos ondas de sonido (fonones) se encuentran y se dispersan, de manera similar a las colisiones en un acelerador de partículas. Cuando un altavoz se ajusta a un cierto límite, de modo que el impulso del fonón es cero, la amplitud resultante puede ser proporcional a una potencia fraccionaria. Este comportamiento de escala, explica el equipo, probablemente no se limita a los fonones en los sólidos, y su reconocimiento puede ayudar al estudio de las amplitudes de dispersión en muchos contextos diferentes, desde la física de partículas hasta la cosmología.
"Las propiedades detalladas de las amplitudes de dispersión se han estudiado recientemente con mucho vigor", afirmó Esposito. "El objetivo de este amplio programa es clasificar los posibles patrones de comportamiento de las amplitudes de dispersión, tanto para hacer que algunos de nuestros cálculos sean más eficientes como más ambiciosos, para construir nuevas bases de la teoría cuántica de campos".
Los diagramas de Feynman han sido durante mucho tiempo una herramienta indispensable para los físicos de partículas, pero tienen ciertas limitaciones. Por ejemplo, los cálculos de alta precisión pueden requerir que se ingresen decenas de miles de diagramas de Feynman en una computadora para describir las interacciones de las partículas. Al obtener una mejor comprensión de las amplitudes de dispersión, los investigadores pueden identificar más fácilmente el comportamiento de las partículas en lugar de confiar en el enfoque de arriba hacia abajo de los diagramas de Feynman, lo que mejora la eficiencia de los cálculos.
"El presente trabajo revela un giro en la historia, mostrando que la física de la materia condensada muestra una fenomenología de amplitudes de dispersión mucho más rica que lo que se vio anteriormente en la física relativista fundamental", agregó Esposito. "El descubrimiento de la escala de potencia fraccionaria invita a seguir trabajando en la dispersión de amplitudes de oscilaciones colectivas de materia, poniendo los sólidos en el centro". Forjando nuevos caminos en la física de partículas