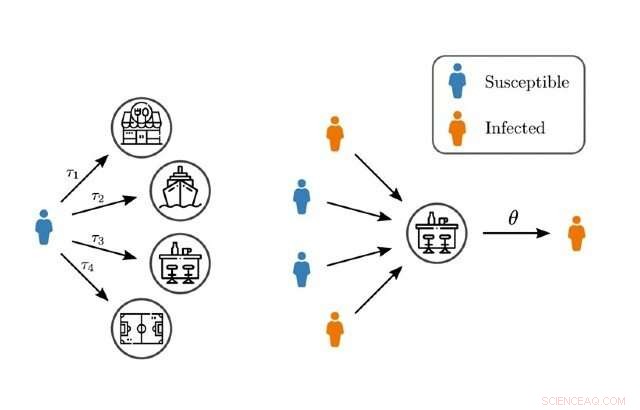
Modelado de contagios y eventos de superpropagación a través de redes de orden superior. Crédito:Queen Mary, Universidad de londres
Los modelos matemáticos se han utilizado ampliamente para orientar las decisiones gubernamentales sobre la pandemia de COVID-19, desde pronosticar resultados hasta incluso probar posibles intervenciones.
Sin embargo, la complejidad de los escenarios del mundo real todavía plantea nuevos desafíos teóricos para la modelización matemática de la propagación de la epidemia.
Por ejemplo, La evidencia de los eventos de superpropagación de COVID-19 indica que es difícil definir las características de estos eventos, que pueden variar significativamente en su duración y número de personas involucradas.
Los modelos de red existentes de propagación de epidemias a menudo se centran en los contactos entre pares de personas mientras comparten la ubicación de las personas, como en el lugar de trabajo, restaurantes, o gimnasio suelen incluir a más de dos personas. A menudo, tampoco consideran las duraciones temporales heterogéneas de estas interacciones en una ubicación específica.
En un nuevo estudio, publicado hoy en Cartas de revisión física , Los investigadores desarrollaron un nuevo enfoque para el modelado de epidemias que considera las interacciones entre dos o más personas en el mismo lugar y durante diferentes períodos de tiempo.
Supuestos desafiantes
El modelo desarrollado por el equipo de investigación internacional, incluidos físicos de la Universidad de Vermont y la Université Laval, y dirigido por la profesora Ginestra Bianconi, matemático de la Universidad Queen Mary de Londres, también tuvo en cuenta la evidencia emergente que sugiere que se requiere una dosis infecciosa mínima para que ocurra una infección.
Este nuevo enfoque de modelado cambia radicalmente los supuestos bien establecidos en el modelado de redes epidémicas, tales como tasas de infección que son lineales con el número de personas infectadas. Los hallazgos muestran que las ubicaciones conjuntas combinadas con una duración heterogénea de la exposición pueden dar lugar a tasas de infección no lineales si se necesita una dosis infecciosa mínima para que ocurra una infección.
Profesora Ginestra Bianconi, Profesor de Matemática Aplicada en Queen Mary, dijo:"La coubicación puede involucrar a grupos de personas, mientras que, por lo general, los modelos de red de propagación de epidemias se basan en redes de contacto que describen interacciones por pares que pueden tener una topología muy diferente a la de las redes de contacto de coubicación. La coubicación también ocurre en el tiempo, por ejemplo, podría ir al mismo gimnasio que otra persona, pero es posible que no siempre nos encontremos y hagamos ejercicio durante diferentes períodos de tiempo ".
"Nuestro enfoque abarca las heterogeneidades de las interacciones debido a la ubicación conjunta que ocurre entre más de dos personas durante diferentes períodos de tiempo y revela que los núcleos de infección pueden ser no lineales en estos escenarios altamente heterogéneos, lo que significa que si hay el doble de personas infectadas que visitan un lugar determinado, la probabilidad de infección también puede ser más del doble. Estos resultados arrojan nueva luz sobre la naturaleza muy heterogénea de los eventos de superpropagación en el contexto de COVID-19 ".