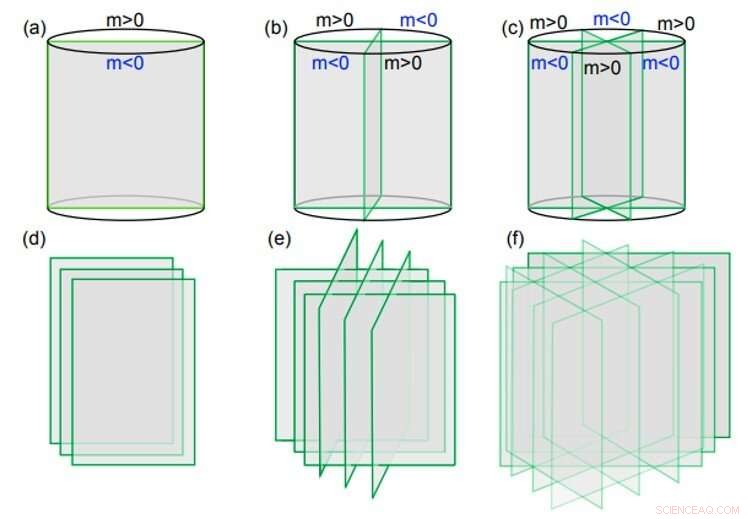
Construcciones en espacio real para C2, 4, Simetrías de 6 rotaciones y de inversión de tiempo. (a-c) mostrar en ausencia de simetrías de traducción, las construcciones mínimas de doble, la simetría de rotación cuádruple y séxtuple protegió los estados topológicos en tres dimensiones, donde cada plano es un estado topológico protegido por simetría interna bidimensional de bosones o fermiones. Si se trata de un aislante topológico bidimensional, los estados resultantes son los aislantes cristalinos topológicos estudiados en el texto. (d-f) son extensiones simples de las construcciones mínimas, construcción de modelos tridimensionales con simetrías de traducción. Crédito:Science Advances, doi:10.1126 / sciadv.aat2374.
En un nuevo informe sobre Avances de la ciencia , Chen Fang y Liang Fu del Laboratorio Nacional de Física de la Materia Condensada de Beijing en China, Instituto Kavli de Ciencias Teóricas y Departamento de Física, Instituto de Tecnología de Massachusetts en los EE. UU. Detallado el descubrimiento de nuevos tipos de anomalías cuánticas en sistemas bidimensionales con simetría de inversión de tiempo (T) (conservación de la entropía) y simetría de rotación discreta; donde una forma retiene la misma estructura después de la rotación por un giro y orden parciales. Luego se dieron cuenta físicamente de estados anómalos en la superficie de nuevas clases de aislantes cristalinos topológicos (TCI) normales al eje de rotación y que soportan un modo helicoidal. La presencia de modos helicoidales les permitió formar un nuevo dispositivo cuántico a partir de un aislante cristalino topológico conocido como nanovarilla helicoidal con conductancia longitudinal cuantificada.
Un solo sabor de fermión relativista sin masa (partículas elementales) puede tener anomalías cuánticas donde la conservación de la corriente de simetría global se rompe a nivel cuántico. Ejemplos bien conocidos incluyen la anomalía quiral de los fermiones de Weyl en tres dimensiones (3-D), y anomalía de paridad en 2-D. En el presente trabajo, Fang y Fu presentaron una nueva anomalía cuántica asociada con la inversión del tiempo (T) y la simetría rotacional discreta (C norte =2, 4, 6). Tales anomalías solo podrían existir en las teorías que rompieron las simetrías de rotación continua en 2-D. Los materiales específicos como los TCI (aislantes cristalinos topológicos) pueden albergar estados de superficie robustos que tienen una dispersión de Dirac (similar al grafeno) en relación con los portadores sin masa. Romper la simetría protectora dentro de tales materiales puede hacer que los portadores adquieran masa.
Formación de nuevas clases de TCI
En las TCI, la topología y la simetría cristalina se entrelazan para formar estados de superficie con características distintas. La ruptura de la simetría cristalina en los TCI puede impartir masa a los fermiones de Dirac sin masa; por lo tanto, la presencia de estados de superficie topológicos protegidos por simetrías cristalinas es una propiedad definitoria de las TCI. Los 230 grupos espaciales previamente identificados que describen todas las posibles simetrías cristalinas permiten muchas clases diferentes de TCI. Los investigadores habían encontrado previamente una clase de TCI protegida por simetría de reflexión en semiconductores IV-VI y otra clase de TCI protegida conjuntamente por reflexión de deslizamiento y simetría de inversión de tiempo dentro de aisladores de gran espacio para formar fermiones experimentales de "reloj de arena". mientras teoriza varias otras clases de TCI.

Los esquemas de los estados sin espacios en dos dimensiones que tienen simetrías de rotación e inversión de tiempo. Hay (A) dos, (B) cuatro, y (C) seis conos de Dirac, relacionados entre sí por dos-, cuatro-, y simetrías de rotación de seis veces, respectivamente, en la primera zona de Brillouin. Los contornos son los límites de las zonas invariantes de Brillouin, a lo largo del cual la fase Berry se cuantifica a cero o π.Crédito:Science Advances, doi:10.1126 / sciadv.aat2374.
El procedimiento de búsqueda estándar para encontrar materiales topológicos implica calcular la estructura de banda de un material en particular para comprender los estados electrónicos, luego, introduzca esta información en una fórmula para revelar si el material es topológico. Además, la estructura de la banda electrónica, conocida como la relación entre la energía de un electrón y su cuasi-momento, puede determinar si un material es un metal o un aislante. Los investigadores habían probado recientemente una teoría para predecir y descubrir experimentalmente tales materiales topológicos. En el presente trabajo, por lo tanto, Fang y col. predijo una nueva clase de TCI protegidas conjuntamente por rotación n-veces y simetría de inversión de tiempo para exhibir estados de superficie topológicos que contienen conos de Dirac sin masa en las superficies superior e inferior.
Entendiendo la anomalía rotacional
El estudio de la anomalía los llevó a teorizar nuevas clases de invariantes de inversión del tiempo (donde las leyes subyacentes no son sensibles a la dirección del tiempo) TCI con C norte =2, 4, 6 simetría de rotación. Estos TCI tenían estados superficiales anómalos en las superficies superior e inferior. Para cada nueva clase de TCI, el equipo construyó el invariante topológico correspondiente en relación con las funciones de onda de Bloch en el espacio de momento. Basado en la reducción dimensional (número de variables aleatorias o atributos bajo consideración) y estados de la pared del dominio (estructuras magnéticas de ancho finito que separan regiones de magnetización uniforme dentro de un material magnético), los científicos proporcionaron además una comprensión unificada del espacio real de estas TCI. Ellos predijeron que varios materiales se darían cuenta de los estados de superficie anómalos protegidos por simetrías de rotación de dos y cuatro veces. Luego, los investigadores propusieron un nuevo dispositivo cuántico basado en las anomalías, conocida como "varilla helicoidal, "realizado con estos nuevos TCI.
Dos estructuras distintas de pseudoespín que conservan C2. La estructura de pseudospin a lo largo del contorno de igual energía para algunos E> 0, en los hamiltonianos efectivos (A) h + (kx, ky) =kxσx + kyσy y (B) h− (kx, ky) =kxσx - kyσy. Se ve que la estructura izquierda tiene simetría de rotación continua y la derecha no; También se ve que la estructura correcta aún conserva la doble rotación. Crédito:Science Advances, doi:10.1126 / sciadv.aat2374. 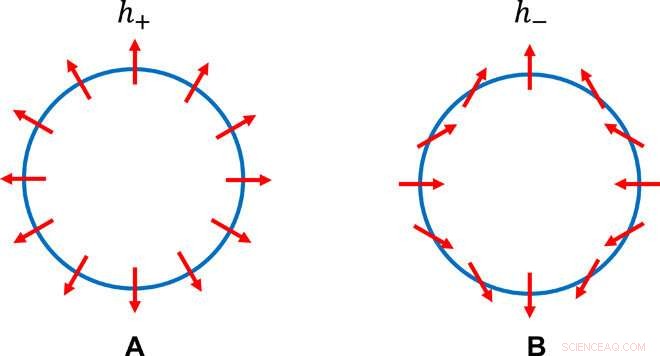
Para construir las nuevas TCI y formar topología en el espacio de impulso, Fang y col. podría agregar dos invariantes de inversión en el tiempo (simetría T), Aisladores topológicos fuertes (TI) cada uno con simetría rotacional n veces mayor. Consideraron la hibridación permitida por la simetría entre los fermiones de Dirac de superficie a los TI para obtener los estados de superficie deseados de los TCI. Los investigadores describieron los fermiones de Dirac utilizando h + yh - Texturas de giro tipo vórtice en el espacio de impulso con quiralidad para diestros y zurdos. Los investigadores observaron la presencia y ausencia de simetría de rotación continua al observar el patrón de vector de pseudospin en algunos contornos de energía iguales de h + yh - respectivamente.
Después de establecer la estructura de bandas del estado de la superficie de TI, Fang y col. proporcionó una explicación alternativa de su naturaleza topológica desde la perspectiva del espacio real, similar a un enfoque de investigación anterior. El enfoque del espacio real agregó perturbaciones permitidas por la simetría para romper la simetría de traslación y separar los fermiones de Dirac sin masa en la superficie para un estudio adicional. Los fenómenos facilitaron estados de TCI no triviales y demostraciones de su robustez bajo interacciones de electrones. Para esto, consideraron un modelo de doble TI de un TCI colocado dentro de un cilindro de un tamaño mayor que la longitud y la superficie de correlación, liso a escala atómica. Para C 4, 6 -TCI colocado en un cilindro, las ubicaciones de los modos en los estados de la superficie no se fijaron a ninguna bisagra física o intersección de superficies cristalinas. Aunque la forma cilíndrica contenía simetría de rotación continua, el sistema descrito en el estudio lo descompuso en simetría rotacional discreta, para indicar la existencia de líneas 1-D sin espacios incluso en un cilindro liso de escala atómica perfectamente.
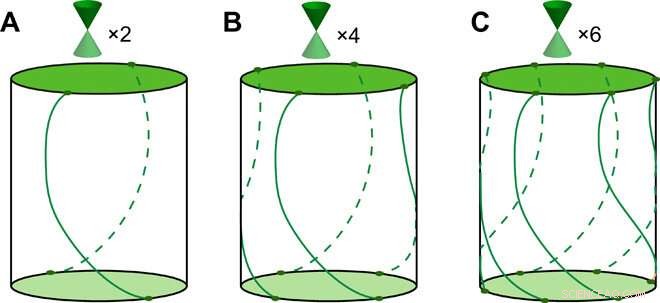
Estados superficiales de rotación TCI. Esquemas de los estados de la superficie en las superficies superior e inferior y los estados de los bordes en las superficies laterales de los nuevos TCI protegidas por (A) doble (B) cuádruple, y (C) simetrías de rotación de seis veces en geometría de varilla. Las superficies superior e inferior tienen conos de Dirac, y en la superficie lateral, dos, cuatro y seis modos de borde helicoidal conectan las dos superficies; pueden tener forma y posición arbitrarias pero están relacionados entre sí por dos-, cuatro-, y seis rotaciones, respectivamente. Crédito:Science Advances, doi:10.1126 / sciadv.aat2374.
Fang y col. luego señaló la posibilidad de comprender los estados cristalinos topológicos desde una perspectiva de reducción dimensional, donde el estado 3-D podría considerarse como un conjunto de capas desacopladas de estados topológicos 2-D. Por tanto, los tres tipos de nuevas TCI introducidas en este trabajo podrían construirse a partir de TI 2-D. Fang y col. utilizaron esta construcción para extender su teoría de estados topológicos protegidos por simetría que interactúan fuertemente protegidos por simetría de rotación y cualquier simetría local, incluyendo, pero no se limita a la simetría de inversión del tiempo.
Dado que se sabe que los modos helicoidales 1-D están libres de retrodispersión debido a la simetría de inversión del tiempo, esta propiedad única permitió a Fang et al. para diseñar una nanovarilla helicoidal a partir de estos nuevos materiales. Cada modo helicoidal solo requería simetría de inversión de tiempo para su protección y la simetría de rotación aseguraba que los modos n-helicoidales no se cruzaran entre sí en el espacio real y se separaran. De este modo, siempre que la simetría de rotación no se rompa considerablemente, estos modos de borde helicoidal permanecerían estables, aunque ya no se relacionaban entre sí a través de una rotación, para formar nuevas clases de TCI con anomalías de rotación en la superficie.
© 2020 Science X Network