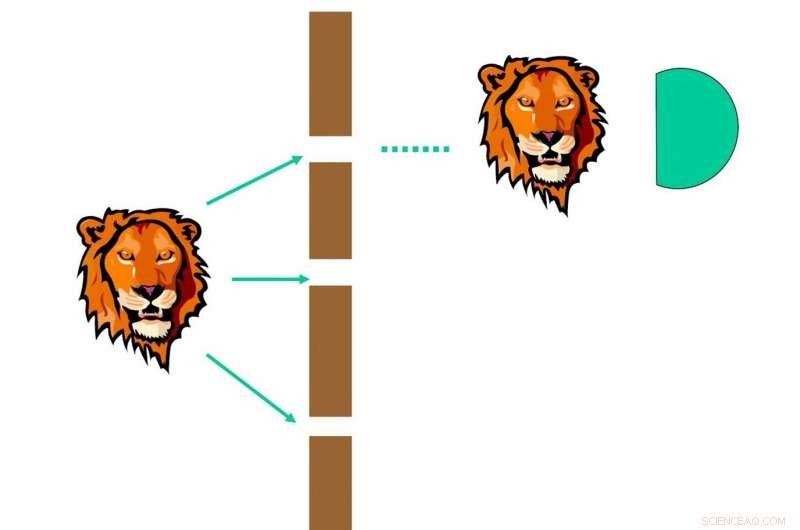
Colapso en una medición parcial. La función de onda completa colapsa en un estado propio cubierto por la función de onda parcial medida con cierta probabilidad, 1/3 en este ejemplo. Crédito:Science China Press
El postulado de la medición es crucial para la mecánica cuántica. Si medimos un sistema cuántico, solo podemos obtener uno de los valores propios del observable medido, como la posición, energía y así sucesivamente, con una probabilidad. Inmediatamente después de la medición, el sistema colapsará instantáneamente en el estado propio correspondiente, conocido como colapso estatal. Se argumenta que el teorema de no clonación es en realidad un resultado del postulado de medición, porque el teorema de la no clonación también se aplicaría a la física clásica. La posibilidad de clonación en la física clásica es en realidad la capacidad de medir completamente un sistema clásico, de modo que se pueda medir y preparar un estado clásico.
Para explicar claramente la medición en mecánica cuántica, es mejor usar el siguiente ejemplo. Supongamos que un fotón pasa a través de tres rendijas idénticas y colocamos un detector ideal y sin demolición después de cada una de las rendijas. Según el postulado de la medición, uno de los detectores detectará el fotón, y como resultado, toda la función de onda colapsará en esa rendija.
¿Qué pasará si colocamos un solo detector después de la rendija superior? Es natural pensar que tendrá un tercio de probabilidad de detectar el fotón, y colapsa toda la función de onda en la ranura 1, como se muestra en la Fig. 2. Sin embargo, ¿Qué pasará si el detector de la rendija superior no mide el fotón? Esta es una medida parcial. Esto se encontró en el formalismo de computación cuántica de dualidad, donde se propuso la combinación lineal de unitarios (LCU) para realizar computación cuántica.
Long propuso que al medir una onda parcial, seguramente sucederá algo:(1) colapso:colapsará en uno de los valores propios con cierta probabilidad. Después de la medición, toda la función de onda cambiará instantáneamente al estado propio correspondiente; (2) colapso:la función de onda medida desaparecerá, y cambie a la parte no medida. Como se muestra en la Fig.2, el detector medirá el fotón con una probabilidad de 1/3, y toda la función de onda del fotón colapsa en la rendija superior. Como se muestra en la Fig.3 para colapso, la parte medida en la hendidura superior desaparece, y la parte no medida, es decir, aumenta la función de onda en la rendija media y la rendija inferior.
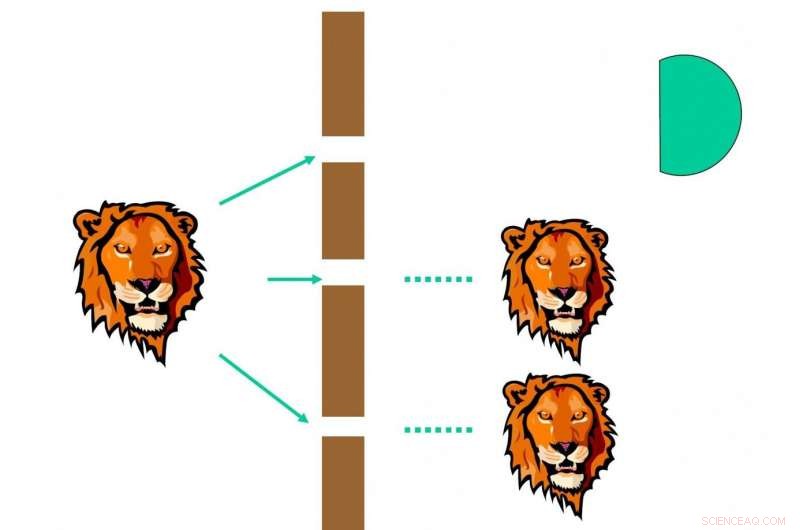
Colapso en una medida parcial. La parte medida en la hendidura superior desaparece, y se incrementa la parte no medida en las ranuras media y baja. Crédito:Science China Press
En realidad, la medición parcial es más común que la medición completa. Cabe señalar que el colapso hacia adentro y hacia afuera de la medición parcial ocurre aleatoriamente no solo en el espacio, pero también con el tiempo. Por ejemplo, la detección de fotones por un detector puede entenderse naturalmente en términos de este postulado de medición parcial. Cuando la función de onda de un fotón pasa a un detector, no se mide en su totalidad al mismo tiempo, es decir, no es una medida completa. Su parte frontal llega primero al detector, golpeando alguna zona del detector. O colapsa en cualquier punto del área de intersección en el detector o colapsa y la probabilidad correspondiente se desplazará a otra parte de la función de onda. Este proceso continúa hasta que se detecta el fotón. Si el fotón no se ha detectado hasta que la última parte de la función de onda llega al detector, luego, la amplitud de esta función de onda restante aumenta a 1 para detectar el fotón con certeza en el paso final.
Esta explicación se da en el punto de vista de que la función de onda es solo la entidad del sistema cuántico en sí, la interpretación WISE. En interpretación WISE, NO hay relación entre la función de onda y el sistema cuántico, la función de onda ES simplemente el sistema cuántico. La interpretación de WISE está respaldada por el experimento de elección retrasada del encuentro, lo cual ha sido reportado en varios medios hace unos años.