
Figura 1. El perfil de intensidad espacial de un rayo láser que se propaga en un medio no lineal se vuelve espontáneamente no uniforme debido al proceso de inestabilidad modulacional. Crédito:Instituto de Ciencias Básicas
Estamos más familiarizados con las cuatro fases convencionales de la materia:sólido, líquido, gas, y plasma. Cambios entre dos fases, conocidas como transiciones de fase, están marcados por cambios abruptos en las propiedades del material, como la densidad. En las últimas décadas se ha dedicado un amplio cuerpo de investigación en física al descubrimiento de nuevas fases no convencionales de la materia, que normalmente emergen a temperaturas ultrabajas o en materiales especialmente estructurados. Las fases "topológicas" exóticas exhiben propiedades que solo pueden cambiar de manera cuantificada (paso a paso), haciéndolos intrínsecamente robustos contra impurezas y defectos.
Además de los estados topológicos de la materia, Las fases topológicas de la luz pueden surgir en ciertos sistemas ópticos, como los cristales fotónicos y las matrices de guías de ondas ópticas. Los estados topológicos de la luz son de interés, ya que pueden formar la base de las futuras tecnologías de comunicación basadas en la luz y energéticamente eficientes, como los láseres y los circuitos ópticos integrados.
Sin embargo, a altas intensidades, la luz puede modificar las propiedades del material subyacente. Un ejemplo de tal fenómeno es el daño que los láseres de alta potencia pueden infligir en los espejos y lentes. Esto a su vez afecta la propagación de la luz, formando un circuito de retroalimentación no lineal. Los efectos ópticos no lineales son esenciales para el funcionamiento de ciertos dispositivos como láseres, pero pueden conducir al surgimiento del desorden del orden en un proceso conocido como inestabilidad modulacional, como se muestra en la Figura 1. Comprender la interacción entre la topología y la no linealidad es un tema fascinante de investigación en curso.
Daniel Leykam, Aleksandra Maluckov, y Sergej Flach en el Centro de Física Teórica de Sistemas Complejos (PCS) dentro del Instituto de Ciencias Básicas (IBS, Corea del Sur), junto con sus colegas Ekaterina Smolina y Daria Smirnova del Instituto de Física Aplicada, Academia de Ciencias de Rusia y Universidad Nacional de Australia, han propuesto un método novedoso para caracterizar las fases topológicas de la luz utilizando inestabilidades no lineales exhibidas por haces de luz brillantes. Esta investigación fue publicada en Cartas de revisión física .
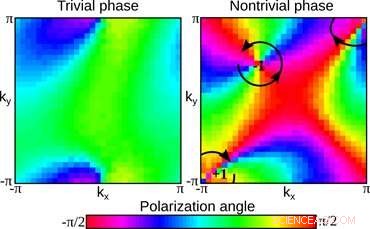
Figura 2. Perfil de polarización de campo lejano de rayos láser después de que se ha desarrollado la inestabilidad modulacional. Las fases topológicas triviales y no triviales se pueden distinguir contando el número de vórtices en el ángulo de polarización. No hay vórtices en la fase trivial (izquierda), y un par de vórtices con carga opuesta en la fase no trivial (derecha). Crédito:Instituto de Ciencias Básicas
En este trabajo, Los investigadores abordaron la cuestión fundamental de cómo las fases topológicas de la luz en medios ópticos no lineales se someten al proceso de inestabilidad modulacional. Teóricamente se demostró que ciertas características de la inestabilidad, como su tasa de crecimiento, puede diferir entre diferentes fases topológicas. Los investigadores realizaron simulaciones numéricas de la inestabilidad modulacional y demostraron que se puede utilizar como herramienta para identificar diferentes fases topológicas de la luz. Un ejemplo de esta idea se muestra en la Figura 2:Mientras que los rayos de luz generados por la inestabilidad tienen patrones de intensidad aparentemente aleatorios, exhiben un orden oculto en su polarización en forma de vórtices robustos. Se cuantifica el número de vórtices que aparecen como resultado de la inestabilidad, y se pueden utilizar para distinguir diferentes fases topológicas.
La forma más común de identificar las fases topológicas de la luz ha sido mirar los bordes del material, donde se localizan ciertas longitudes de onda ópticas. Sin embargo, una caracterización completa requiere medir las propiedades generales del material, que es una tarea mucho más difícil. La luz del material a granel sufre una complicada interferencia de ondas y es muy sensible a los defectos. que oscurece sus propiedades topológicas. Contraintuitivamente, Los investigadores han demostrado cómo se pueden utilizar las inestabilidades no lineales para controlar esta interferencia no deseada y codificar espontáneamente las propiedades topológicas del material en haces de luz. Este enfoque proporciona una forma más sencilla de sondear y quizás incluso generar estados topológicos de luz.
El siguiente paso será probar esta propuesta en un experimento. Por ejemplo, Las matrices de guías de ondas ópticas inscritas en un vidrio serán una plataforma ideal para este propósito. Al hacer brillar un rayo láser pulsado brillante en el vidrio, Debería ser posible observar directamente la inestabilidad modulacional y así medir las propiedades topológicas de la matriz de guías de ondas. Actualmente, el grupo de investigación está discutiendo con colaboradores posibles diseños para la verificación experimental de su teoría.