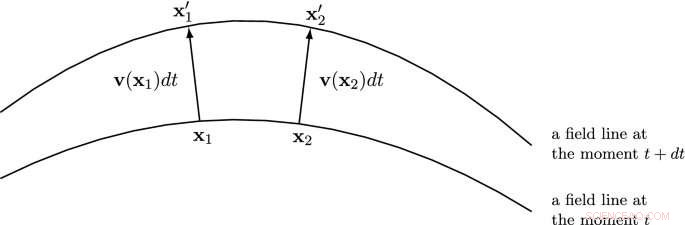
La imagen demuestra la condición que el campo vectorial v debe obedecer para definir la evolución temporal autoconsistente de las líneas de campo. Para dos puntos cualesquiera en una línea de campo en el momento t, los extremos de los vectores vdt en los puntos correspondientes se encuentran en una línea de campo que se define en el momento t + dt DOI 10.1140 / epjc / s10052-020-08745-7
Las ecuaciones de Maxwell gobiernan la evolución de los campos electromagnéticos siendo la luz una solución particular de estas ecuaciones en espacios desprovistos de carga eléctrica. Un nuevo estudio publicado en EPJ C por Alexi Morozov y Nikita Tselousov, del Instituto de Física y Tecnología de Moscú y del Instituto de Problemas de Transmisión, Rusia, respectivamente, detalla soluciones peculiares a las ecuaciones de Maxwell, los llamados nudos de Maxwell. La investigación podría tener aplicaciones en los campos de la física matemática y la teoría de cuerdas.
“Por lo general, pensamos en la luz como ondas planas. Fue un gran avance cuando se descubrieron soluciones de luz 'anudadas', "explica Tselousov." La naturaleza de nudos de estas soluciones consiste en la estructura de las líneas de campo eléctrico y magnético. Se puede observar que algunas de las líneas de campo son lazos cerrados y no trivialmente anudados ".
Las líneas de campo eléctrico y magnético cambian con el tiempo obedeciendo a las ecuaciones de Maxwell. A medida que los campos cambian, sus líneas de campo se mueven de alguna manera en el espacio. Si bien los investigadores no pueden rastrear una línea de campo arbitraria, Las líneas de campo cerrado son especiales y se pueden observar a medida que evolucionan con el tiempo.
"En nuestro periódico, hacemos una conjetura, que las líneas de campo anudadas se mueven de una manera muy especial en la que la estructura anudada permanece, "Tselousov continúa". En otras palabras, se puede decir que esta vez la evolución nunca implica autocruces o cruces de dos líneas de campo ".
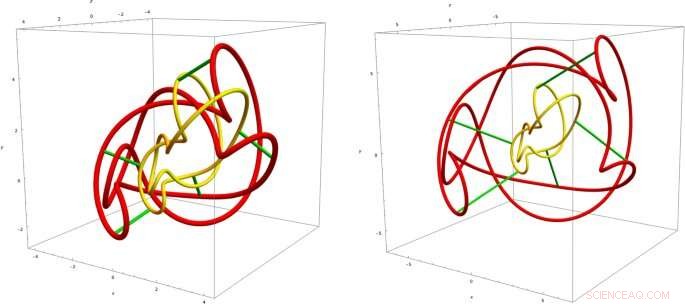
El pequeño nudo amarillo se convierte en el gran nudo rojo con la evolución del tiempo. Hay imágenes de dos momentos sucesivos. Las curvas verdes son las trayectorias. La estructura topológica del nudo no cambia con la evolución temporal DOI 10.1140 / epjc / s10052-020-08745-7
Tselousov cree que si esta conjetura, a la que se llegó con el uso de complejas simulaciones por computadora, sería correcta, la conservación de los nudos implica que su evolución es integrable, capaz de sufrir la integración de la función matemática. Esto significa que su evolución puede relacionarse con otros modelos y sistemas, en particular con ecuaciones no lineales, que se sabe que comparten esta propiedad.
"Es muy raro y siempre es un placer observar las propiedades integrables de los sistemas porque significa una comprensión más profunda y un posible progreso adicional. Planeamos avanzar en esta dirección y encontrar más conexiones con la integrabilidad, "Tselousov concluye." En mi mente, uno de los hechos asombrosos es esa luz, tan familiar para todos, ocultar secretos que solíamos ignorar durante siglos ".
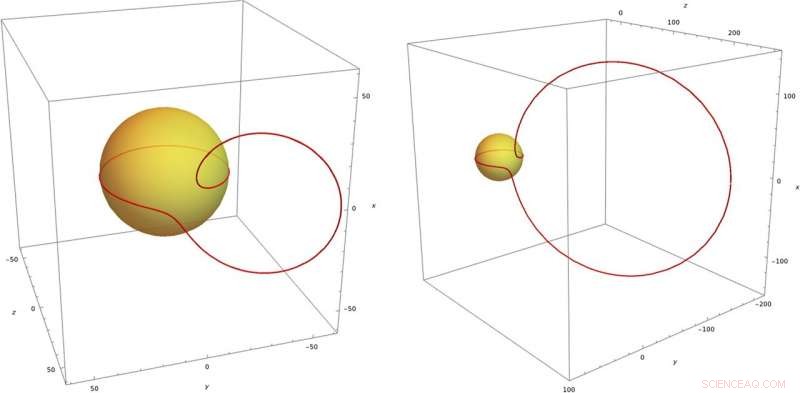
La esfera amarilla es el cono de luz x2 + y2 + z2 =t2x2 + y2 + z2 =t2. Las líneas rojas son líneas de campo eléctrico en el momento t =30t =30. Una parte de la línea de campo se encuentra en el ecuador de la esfera. La otra parte tiende a formar un círculo DOI 10.1140 / epjc / s10052-020-08745-7