Dada una lista de ciudades y las distancias entre cada par de ciudades, ¿Cómo se determina la ruta más corta que visita cada ciudad exactamente una vez y regresa al lugar de partida? Este famoso problema se denomina "problema del viajante de comercio" y es un ejemplo de un problema de optimización combinatoria. Resolver estos problemas con computadoras convencionales puede llevar mucho tiempo, y para este propósito se han creado dispositivos especiales llamados "templadores cuánticos".

Los atemperadores cuánticos están diseñados para encontrar el estado de energía más bajo (o estado fundamental) de lo que se conoce como modelo de Ising. Dichos modelos son representaciones abstractas de un sistema mecánico cuántico que involucra espines interactivos que también están influenciados por campos magnéticos externos. A finales de los 90, Los científicos descubrieron que los problemas de optimización combinatoria se podían formular como modelos de Ising, que a su vez podría implementarse físicamente en los templados cuánticos. Para obtener la solución a un problema de optimización combinatoria, uno simplemente tiene que observar el estado fundamental alcanzado en su templador cuántico asociado después de un corto período de tiempo.

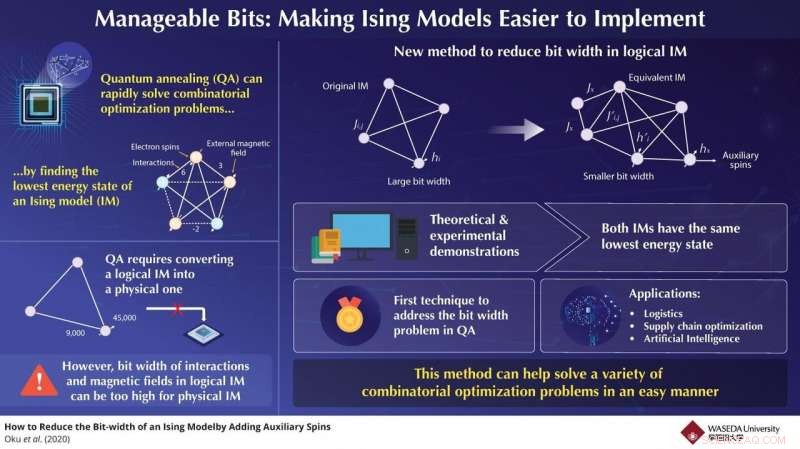
Uno de los mayores desafíos en este proceso es la transformación del modelo de Ising lógico en un modelo de Ising físicamente implementable adecuado para el recocido cuántico. Algunas veces, los valores numéricos de las interacciones de espín o los campos magnéticos externos requieren un número de bits para representarlos (ancho de bits) demasiado grandes para un sistema físico. Esto limita severamente la versatilidad y aplicabilidad de los recocidos cuánticos a problemas del mundo real. Afortunadamente, en un estudio reciente publicado en Transacciones IEEE en computadoras , Los científicos de Japón han abordado este problema. Basado puramente en la teoría matemática, desarrollaron un método mediante el cual un modelo lógico de Ising dado se puede transformar en un modelo equivalente con un ancho de bits deseado para que se ajuste a una implementación física deseada.

Su enfoque consiste en agregar espines auxiliares al modelo de Ising para interacciones problemáticas o campos magnéticos de tal manera que el estado fundamental (solución) del modelo transformado sea el mismo que el del modelo original y al mismo tiempo requiera un ancho de bit menor. La técnica es relativamente simple y está completamente garantizada para producir un modelo Ising equivalente con la misma solución que el original. "Nuestra estrategia es la primera del mundo en abordar de manera eficiente y teórica el problema de reducción del ancho de bits en las interacciones de espín y los coeficientes de campo magnético en los modelos de Ising, "comenta el profesor Nozomu Togawa de la Universidad de Waseda, Japón, quien dirigió el estudio.

Los científicos también pusieron a prueba su método en varios experimentos, que confirmó aún más su validez. El profesor Togawa tiene grandes esperanzas, y concluye diciendo, "El enfoque desarrollado en este estudio ampliará la aplicabilidad de los atemperadores cuánticos y los hará mucho más atractivos para las personas que se ocupan no solo de los modelos físicos de Ising, sino de todo tipo de problemas de optimización combinatoria. Estos problemas son comunes en la criptografía, logística, e inteligencia artificial, entre muchos otros campos ".