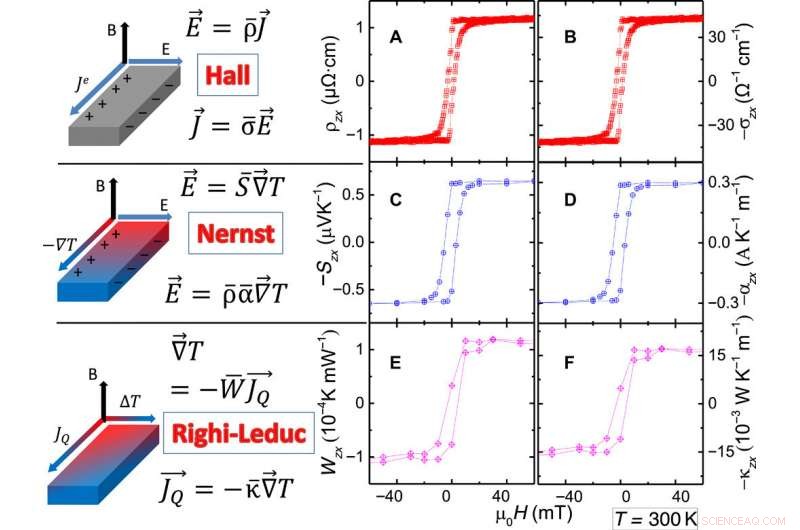
Coeficientes transversales anómalos, definiciones, y perfiles:Componentes fuera de la diagonal de los tres tensores de conductividad [eléctricos (σ̄), termoeléctrico (ᾱ), y térmico (κ̄)] puede ser finito en ausencia de campo magnético. Como se muestra en los tres paneles de la izquierda, se vinculan a cuatro vectores, que son corriente de densidad de carga (J →), campo eléctrico (E →), gradiente térmico (∇ → T), y corriente de densidad de calor (JQ− →). (A) Resistividad Hall (ρzx). (B) Conductividad Hall (σzx) extraída de ρzx, ρxx, y ρzz. (C) Señal de Nernst (Szx). (D) Conductividad termoeléctrica transversal (αzx) extraída de Szx, Sxx, ρxx, ρzz, y ρzx. (E) Resistividad térmica Hall (Wzx). (F) Conductividad térmica Hall o el coeficiente de Righi-Leduc (κzx) extraído de resistividades térmicas diagonales y fuera de la diagonal. Crédito:Science Advances, doi:10.1126 / sciadv.aaz3522
Según la ley de Wiedemann-Franz (WF), la conductividad eléctrica de un metal está vinculada a su contraparte térmica, siempre que el calor transportado por los fonones sea insignificante y los electrones no sufran una dispersión inelástica. En un semimetal Weyl tipo II también conocido como cuarto fermión, la dependencia térmica de la relación entre la conductividad eléctrica y térmica destaca las desviaciones de la ley de Wiedemann-Franz. Los físicos han probado la ley WF en numerosos sólidos, pero tienen la intención de comprender el alcance de su relevancia durante el transporte transversal anómalo e investigar la naturaleza topológica de la función de onda. En un nuevo informe, Liangcai Xu y un equipo de investigación internacional en física de materia condensada en China, Francia, Israel y Alemania, presentó un estudio de la respuesta transversal anómala en un semimetal de Weyl antiferromagnético no colineal, Minnesota 3 Ge. Variaron las condiciones experimentales desde la temperatura ambiente hasta la temperatura sub-Kelvin y observaron una violación de la correlación WF por temperatura finita. Atribuyeron el resultado a un desajuste entre las sumas térmicas y eléctricas de la curvatura Berry (una fase geométrica adquirida en el transcurso de un ciclo) y no debido a la dispersión inelástica. El equipo respaldó su interpretación con cálculos teóricos para revelar una competencia entre la temperatura y la distribución de la curvatura de Berry. El trabajo ahora está publicado en Avances de la ciencia .
La curvatura de Berry de los electrones puede resultar en el efecto Hall anómalo (AHE) si el sólido anfitrión carece de simetría de inversión del tiempo (conservación de la entropía). Si bien las contrapartes termoeléctricas y térmicas del efecto Hall anómalo se exploran con menos frecuencia, ellos también surgen de los mismos campos magnéticos ficticios. Queda por determinar cómo se correlacionan entre sí las magnitudes de tales coeficientes fuera de la diagonal anómalos y si las correlaciones establecidas entre los coeficientes de transporte ordinarios continúan siendo válidas. Actualmente es laborioso formar una fórmula semiclásica del efecto Hall anómalo (AHE), por lo tanto, cualquier imagen intuitiva de producir un campo eléctrico transversal es aún más desafiante. En este trabajo, el equipo de investigación presentó un estudio de un sólido magnético, se centró en la relación entre conductividades Hall eléctricas y térmicas anómalas. Xu y col. determinó las variables en un amplio rango de temperatura, para incluir la relación de Lorenz anómala (L A ij ) y el valor de Sommerfeld (L 0 ), que permanecieron cerca el uno del otro, sin embargo, una desviación comenzó por encima de 100 K. El equipo afirmó que la observación implicaba un mecanismo hasta ahora no observado para la violación de temperatura finita de la ley WF. Como resultado, apoyaron observaciones experimentales en el estudio con cálculos teóricos para identificar la curvatura Berry de la familia semimetálica Weyl (Mn 3 Ge y Mn 3 Sn).
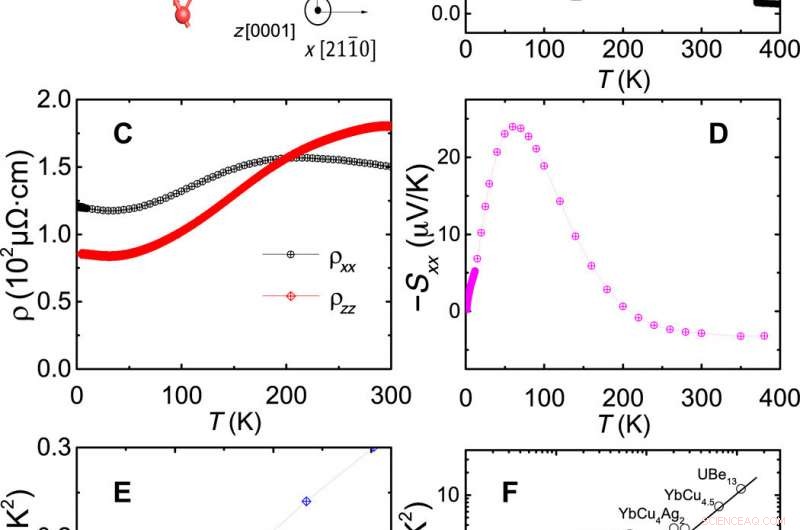
Antiferromagnético, sucio, y correlacionados. (A) Un bosquejo de la textura magnética de Mn3Ge, mostrando la orientación de los espines de los átomos de Mn. El rojo y el azul representan dos planos adyacentes. (B) Dependencia de la temperatura de la magnetización con la temperatura de Néel visible a 370 K. emu, Unidad electromagnética. (C) Dependencia de la resistividad con la temperatura a lo largo de dos orientaciones. (D) El coeficiente de Seebeck, S, en función de la temperatura. (E) Calor específico de baja temperatura, CONNECTICUT, en función de T2. La extrapolación a T =0 produce γ =24,3 mJ mol − 1 K − 2. (F) Gráfico del valor absoluto de S / T frente a γ para varios metales correlacionados, incluidos Mn3X y MnSi. Crédito:Science Advances, doi:10.1126 / sciadv.aaz3522
Basado en proposiciones teóricas, el equipo observó un gran efecto Hall anómalo en Mn 3 X (donde X es igual a Sn y Ge) familia de antiferromagnetos no colineales por debajo de una temperatura de Néel, es decir, que refleja la no linealidad de los materiales superparamagnéticos en campos bajos. Los resultados proporcionaron un perfil distinto de la resistividad de Hall y un método sencillo para extraer la conductividad anómala con los recién llegados (Mn 3 Ge y Mn 3 Sn) en el campo emergente de la espintrónica antiferromagnética. Los científicos incluso siguieron el destino de las señales en Mn. 3 Baje a temperaturas sub-Kelvin en el estudio para comprender el fenómeno.
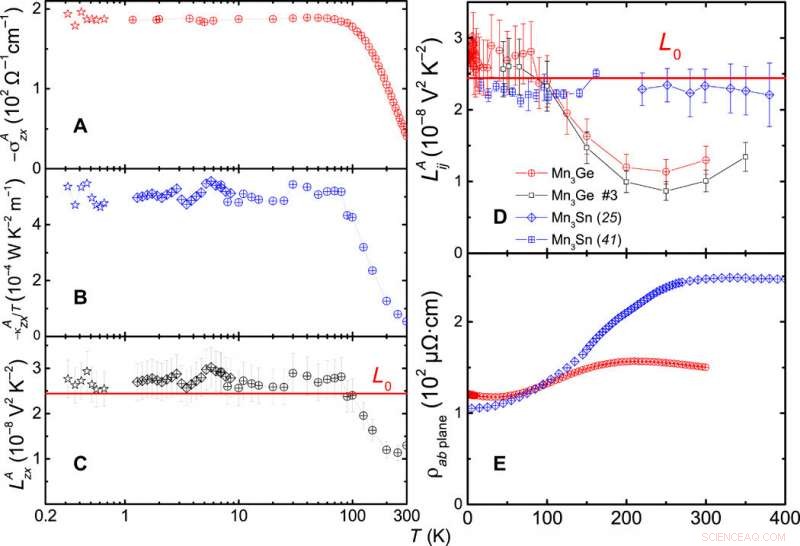
Ley de WF transversal anómala. Dependencia de la temperatura de la conductividad Hall anómala σAzx (A), la conductividad térmica anómala de Hall dividida por la temperatura κAzx / T (B), y (C) la relación de Lorenz anómala κAzx / σAzxT. Se utilizan diferentes símbolos para los datos obtenidos con dos configuraciones diferentes:termómetros resistivos (diamantes) y termopares (círculos). Los símbolos de estrella se refieren a un tercer conjunto de datos obtenidos en otra muestra medida hasta temperaturas sub-kelvin. La línea continua horizontal marca L0 =2.44 × 10−8 V2 K − 2. La desviación entre L y L0 comienza en T> 100 K y es concomitante con la disminución de σAzx. (D) Dependencia de la temperatura de la relación de Lorenz anómala en Mn3Ge y en Mn3Sn. Mn3Ge # 3 muestra un repunte a alta temperatura. Los datos de Hall se pueden encontrar en los Materiales suplementarios. (E) Comparación de su resistividad en el plano. La gran desviación de la ley WF en Mn3Ge ocurre a pesar de que la dependencia de la temperatura de su resistividad es incluso más modesta que la de Mn3Sn. Crédito:Science Advances, doi:10.1126 / sciadv.aaz3522
Midieron la resistividad de Hall, Señal de Nernst (fenómeno termoeléctrico o termomagnético observado en una muestra conductora de electricidad, sujeta a un campo magnético) y resistividad Hall térmica para extraer conductividades Hall eléctricas / termoeléctricas y térmicas. Observaron propiedades básicas del sistema, incluida la textura de giro, magnetización y resistividad eléctrica para mostrar poca variación con la temperatura. Xu y col. detalló la ley de WF transversal anómala como el principal hallazgo del estudio. Por ejemplo, por debajo de 100 K, la relación de Lorenz anómala fue plana con una magnitud ligeramente mayor que el valor de Sommerfeld. Por encima de 100 K, la relación de Lorenz anómala en Mn 3 Ge y Mn 3 Sn se comportó de manera muy diferente pero su resistividad solo mostró un ligero cambio con la temperatura, en contraste con los ferromagnetos elementales.
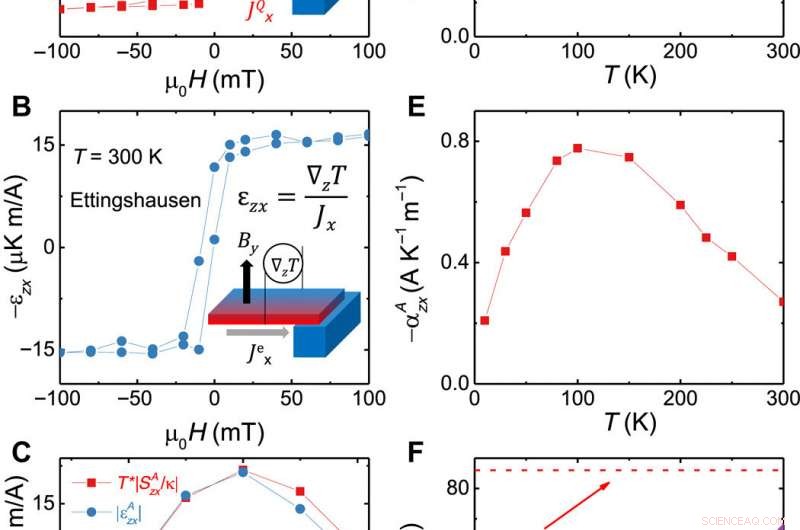
Efectos anómalos de Nernst y Ettingshausen y la relación de Bridgman. (A) El campo eléctrico transversal creado por un gradiente de temperatura longitudinal finito en función del campo magnético (el efecto Nernst). (B) El gradiente térmico transversal producido por una corriente de carga longitudinal finita (el efecto Ettingshausen) a la misma temperatura. Los recuadros muestran configuraciones experimentales. (C) La dependencia de la temperatura de los coeficientes anómalos de Nernst (SAzx) y de Ettingshausen (ϵAzx) anómalos. ϵAzx y SAzxT / κxx permanecen iguales según lo esperado por la relación de Bridgman. (D y E) Dependencia de la temperatura de σAzx y αAzx extraídas de la señal de Hall y la señal de Nernst SAzx. (F) La evolución de la relación de αAzx / σAzx con la temperatura. Crédito:Science Advances, doi:10.1126 / sciadv.aaz3522
Dado que varias proposiciones anteriores sobre la violación de la ley WF fueron refutadas posteriormente, los nuevos datos tenían que ser validados por criterios independientes. Los científicos apoyaron la validez de su trabajo al verificar la relación de Kelvin (para coeficientes de transporte normales) y la relación de Bridgman (para coeficientes transversales anómalos). Basado en la termodinámica de procesos irreversibles, las relaciones tenían que seguir siendo válidas independientemente de los detalles microscópicos. Xu y col. por lo tanto incorporó los mismos datos (campo eléctrico y gradiente térmico) para estudios térmicos y termoeléctricos y la validez resultante de las relaciones de Kelvin y Bridgman en el trabajo garantizó la validez de los datos térmicos recolectados como confirmación experimental adicional.
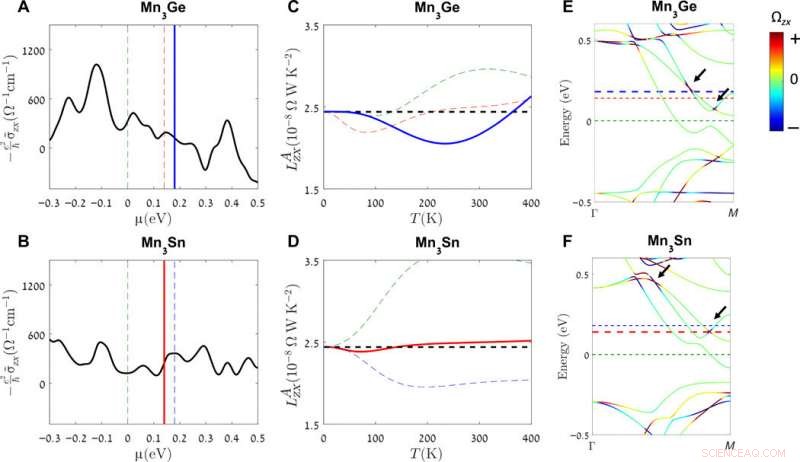
Contrastando el espectro teórico de Berry en Mn3Ge y en Mn3Sn. La curvatura teórica de Berry a temperatura cero σ∼zx (μ) (A y B) y la relación de Lorenz anómala LAzx (C y D). El punto neutro de carga se establece en cero. El verde, rojo, y las líneas azules representan μ =0, 140, y 180 meV, respectivamente. Las líneas negras horizontales discontinuas representan L0 en (C) y (D). En la estructura de bandas (E y F), el color indica el valor de curvatura de Berry. Las flechas azules señalan dos puntos Weyl entre la banda de conducción más baja y la segunda más baja. Crédito:Science Advances, doi:10.1126 / sciadv.aaz3522
La ley WF también puede dejar de ser válida en presencia de dispersión inelástica, dado que la colisión inelástica de ángulo pequeño puede disminuir el flujo de impulso. Cuando el equipo examinó el caso de Mn 3 X metales en relación con la ley WF concluyeron los mecanismos de dispersión dominantes tanto en Mn 3 Sn y Mn 3 Se basará en la dispersión de los defectos antisitio (defectos cristalográficos). Había poco espacio para la dispersión inelástica en el estudio, destacando el requisito de una ruta alternativa hacia la violación observada de la ley WF. La teoría resultante mostró cualitativamente los diferentes espectros de Berry en Mn 3 Sn y Mn 3 Ge, que conducen a diferentes comportamientos a temperatura finita para los dos compuestos; cumpliendo así el requisito de ruta alternativa y validando aún más el resultado del estudio.
De este modo, Liangcai Xu y sus colegas midieron las contrapartes del efecto Hall anómalo asociado con el flujo de entropía. Descubrieron que la ley de WF que vincula los efectos Hall térmicos y eléctricos es válida a temperatura cero, aunque surgió una desviación finita por encima de 100 K. El efecto de dispersión dominante en el estudio fue elástico y propusieron que la desviación resultara de un desajuste en las sumas térmicas y eléctricas de la curvatura de Berry junto con los cálculos teóricos, que además apoyó el trabajo.
© 2020 Science X Network