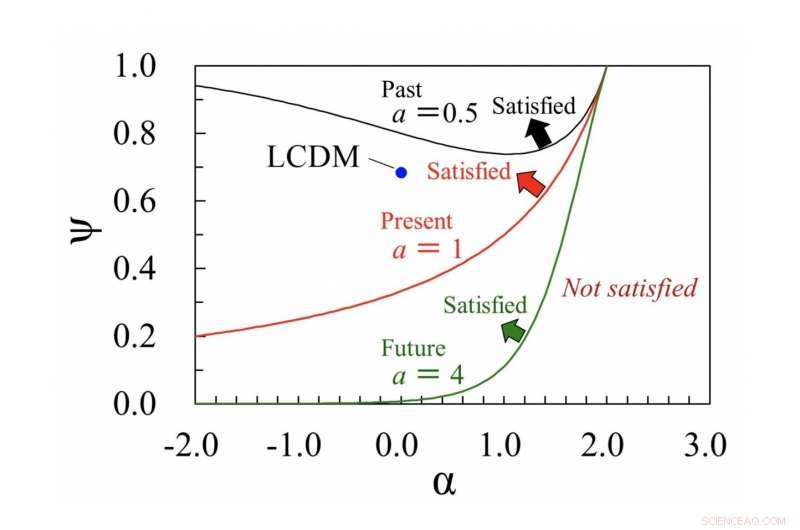
La Figura 1 muestra el límite para la maximización de la entropía en el ( α , ψ) plano para tres valores del factor de escala normalizado a . ψ representa un tipo de parámetro de densidad para la energía oscura efectiva y α es un exponente del término de ley de potencias H α . El círculo cerrado representa el resultado del modelo LCDM ajustado, es decir., ( α , ψ) =(0, 0,685). Tres límites para los valores de a =0,5, 1, y se muestran 4, dónde a =1 corresponde a la actualidad. La flecha en cada límite indica una región que satisface las condiciones para maximizar la entropía. Esta región se extiende gradualmente hacia abajo a medida que aumenta el factor de escala normalizado. Sin embargo, la región no supera actualmente α =2. Crédito:Universidad de Kanazawa
La expansión del Universo ha ocupado las mentes de astrónomos y astrofísicos durante décadas. Entre los modelos cosmológicos que se han sugerido a lo largo de los años, Los modelos Lambda de materia oscura fría (LCDM) son los modelos más simples que pueden proporcionar explicaciones elegantes de las propiedades del Universo, p.ej., la expansión acelerada del Universo tardío y las formaciones estructurales. Sin embargo, el modelo LCDM adolece de varias dificultades teóricas, como el problema de la constante cosmológica. Para resolver estas dificultades, Recientemente se han propuesto escenarios termodinámicos alternativos que amplían el concepto de termodinámica de los agujeros negros.
"Investigaciones anteriores implican que cierto tipo de universo se comportará como un sistema macroscópico ordinario. Se considera que la expansión del Universo probablemente esté relacionada con la termodinámica en su horizonte, basado en el principio holográfico, "explica el autor del estudio, Nobuyoshi Komatsu de la Universidad de Kanazawa.
"Consideré un modelo cosmológico con un término de ley de potencias, asumiendo la aplicación de la ley de equipartición holográfica. El término de la ley de potencias es proporcional a H α , dónde H es el parámetro de Hubble y α se considera un parámetro libre ( α puede estar relacionado con el entrelazamiento de los campos cuánticos cerca del horizonte) ".
"Usé el modelo propuesto para estudiar las propiedades termodinámicas en el horizonte del Universo, centrándose en las evoluciones de la entropía de Bekenstein-Hawking. Descubrí que el modelo satisface la segunda ley de la termodinámica en el horizonte, "dice el profesor asociado Komatsu.
"Además, Usé el modelo para examinar los procesos similares a la relajación que ocurren antes de la última etapa de la evolución del Universo y así permitir el estudio de la maximización de la entropía ".
"La Figura 1 muestra los límites para la maximización de la entropía en el ( α , ψ) plano. Aquí, ψ representa un tipo de parámetro de densidad para la energía oscura efectiva. El lado superior de cada límite corresponde a la región que satisface las condiciones para la maximización de la entropía. Por ejemplo, Se encuentra que el punto para el modelo LCDM ajustado con precisión satisface las condiciones para la maximización de la entropía en el momento actual. Además, la región cercana a este punto también satisface las condiciones para la maximización de la entropía, tanto en la actualidad como en el futuro. Es probable que los modelos cosmológicos en esta región se vean favorecidos desde el punto de vista de la termodinámica, "dice el profesor asociado Komatsu.
Además de los resultados informados del estudio, Se espera que el modelo desarrollado sirva para permitir la discusión y el análisis de la amplia gama de modelos cosmológicos actualmente disponibles desde una perspectiva termodinámica.