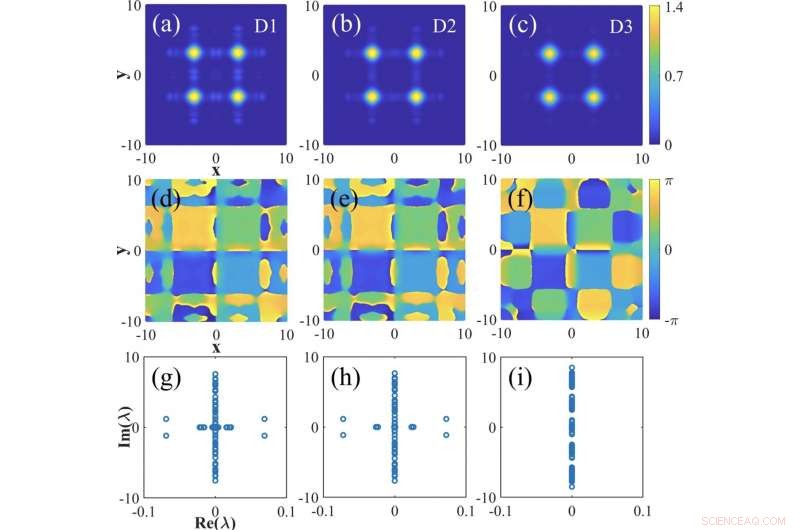
Gráficos de contorno, etapas, y valores propios de los solitones de hueco de vórtice que aparecen como estados enlazados de modo cuádruple. Crédito:XIOPM
Los solitones son objetos estables equilibrados por difracción o dispersión y no linealidad. Un desafío fundamental en este campo es la estabilización de solitones en coordenadas multidimensionales, dado que los solitones 2-D y 3-D en el espacio libre son siempre inestables y sufren, respectivamente, colapsos críticos que surgen de la no linealidad catastrófica de autoenfoque.
La estabilización de estados localizados multidimensionales generalmente se basa en medios periódicos lineales con no linealidad uniforme. Aunque las celosías no lineales con una variación suave de no linealidad pueden admitir varias especies de solitones. Sin embargo, Las propiedades de existencia y estabilidad de los solitones con no linealidades cúbico-quínticas y potencial periódico lineal 2-D aún no se han revelado. ¿Existe algún modelo o método para evitar el colapso crítico de solitones de orden superior?
Un equipo de investigación dirigido por el Prof.Dr. Zeng Jianhua del Instituto Xi'an de Óptica y Mecánica de Precisión (XIOPM) de la Academia China de Ciencias (CAS) propone un esquema factible para estabilizar los modos localizados 2-D contra el colapso crítico considerando el el orden de difracción fraccional para la propagación de la luz en sistemas físicos periódicos con no linealidades de autoenfoque y autodesenfoque en competencia en términos cúbico-cuánticos no lineales. El resultado fue publicado en Física de las comunicaciones .
Proponen teóricamente un marco de ecuación de Schrödinger fraccional no lineal 2-D (NLFSE), que puede reprimir el colapso crítico. Revelan que el modelo produce una variedad de familias de solitones estables, incluidos los solitones verticales y de brecha fundamental 2-D, así como los grupos de solitones de brecha (los solitones siempre son inestables en el modelo de solo quínticos).
Una visión detallada de las propiedades dinámicas de los solitones muestra además que los solitones son robustamente estables en el medio de los huecos de banda del espectro de Bloch lineal subyacente, aunque inestable cerca de los bordes de los espacios de la banda; y la estabilidad de los solitones está moderadamente influenciada por la resistencia no lineal.
El notable descubrimiento ofrece una nueva vía para investigar la existencia y las propiedades dinámicas de los modos localizados 2-D mediante la gestión del orden de difracción y los intervalos de banda sintonizables de los sistemas físicos periódicos.