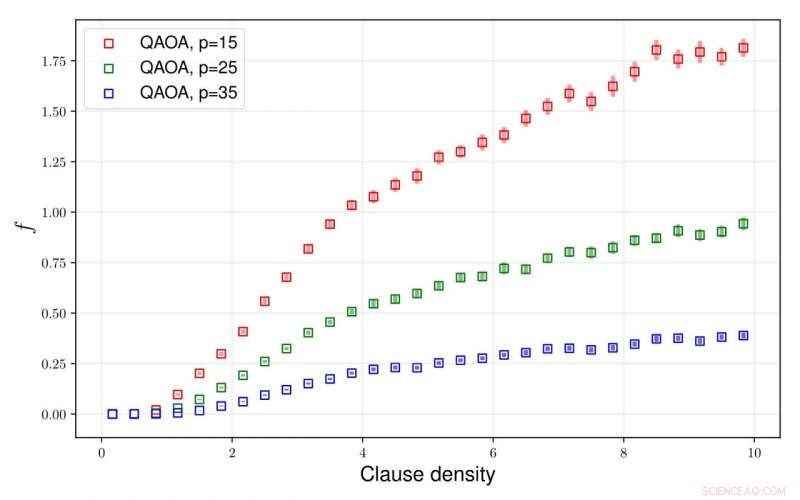
El gráfico representa el rendimiento (diferencia entre los óptimos QAOA y los óptimos exactos) de los circuitos QAOA de profundidad fija en instancias MAX-SAT generadas aleatoriamente con densidades de problemas crecientes. Aunque las versiones de mayor profundidad logran mejores rendimientos, todavía presentan déficits de accesibilidad. Crédito: Cartas de revisión física
Google se apresura a desarrollar procesadores mejorados cuánticamente que utilizan efectos mecánicos cuánticos para aumentar la velocidad a la que se pueden procesar los datos. En el corto plazo, Google ha diseñado nuevos algoritmos mejorados cuánticamente que operan en presencia de ruido realista. El llamado algoritmo de optimización aproximada cuántica, o QAOA para abreviar, es la piedra angular de un impulso moderno hacia el desarrollo de algoritmos mejorados cuánticos y tolerantes al ruido.
El célebre enfoque adoptado por Google en QAOA ha despertado un gran interés comercial y ha encendido una comunidad de investigación global para explorar aplicaciones novedosas. Todavía, Se sabe poco sobre las limitaciones de rendimiento definitivas del algoritmo QAOA de Google.
Un equipo de científicos del Deep Quantum Laboratory de Skoltech asumió este desafío contemporáneo. El equipo de Skoltech dirigido por el profesor Jacob Biamonte descubrió y cuantificó lo que parece ser una limitación fundamental en el enfoque ampliamente adoptado iniciado por Google.
Reportando en Cartas de revisión física , los autores detallan el descubrimiento de los llamados déficits de accesibilidad; los autores muestran que estos déficits imponen una limitación fundamental a la capacidad de QAOA para incluso aproximar una solución a un problema, ejemplo.
Los hallazgos del equipo de Skoltech informan una clara limitación del algoritmo cuántico variacional QAOA. QAOA y otros algoritmos cuánticos variacionales han demostrado ser extremadamente difíciles de analizar utilizando técnicas matemáticas conocidas debido a un proceso interno de retroalimentación cuántica a clásica. A saber, un cálculo cuántico determinado solo puede ejecutarse durante un período de tiempo fijo. Dentro de este tiempo fijo se puede ejecutar un número fijo de operaciones cuánticas. QAOA busca utilizar estas operaciones cuánticas de forma iterativa formando una secuencia de aproximaciones cada vez más óptimas para minimizar una función objetivo. El estudio pone nuevos límites a este proceso.
Los autores descubrieron que la capacidad de QAOA para aproximar soluciones óptimas para cualquier circuito cuántico de profundidad fija depende fundamentalmente de los problemas de "densidad". En el caso del problema denominado MAX-SAT, la denominada densidad se puede definir como la relación entre las limitaciones del problema y el recuento de variables. Esto a veces se denomina densidad de cláusulas.
Los autores descubrieron casos problemáticos de alta densidad con soluciones óptimas que no pueden aproximarse con éxito garantizado. independientemente del tiempo de ejecución del algoritmo.