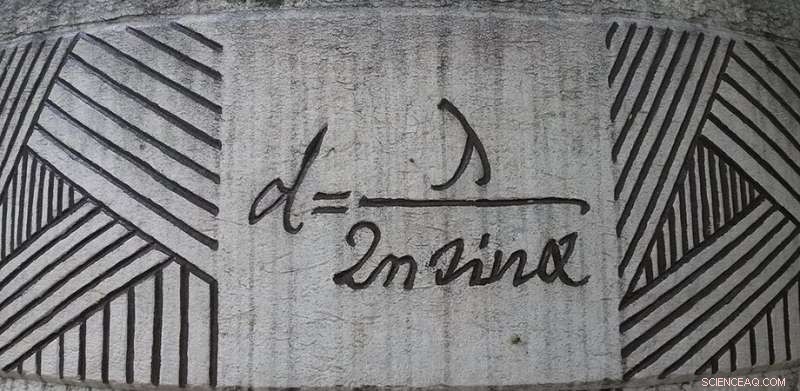
Ecuación de difracción de Ernst Abbe en exhibición en Jena, Alemania. Crédito:Daniel Mietchen, Wikimedia, commons.wikimedia.org/wiki/File:Ernst-Abbe-Denkmal_Jena_F%C3%BCrstengraben_-_20140802_125709.jpg
Aunque nos dicen que una imagen vale más que mil palabras ese cliché subestima seriamente el valor de una buena imagen. Nuestra comprensión de cómo funciona el mundo se simplifica gracias a nuestra capacidad para convertir datos en imágenes. Las imágenes están en el corazón de la ciencia:si se pueden medir, se convertirá en una imagen para analizar.
El factor limitante de las imágenes es la resolución. ¿Qué tan cerca pueden estar dos objetos antes de que un sistema de imágenes los reduzca a un solo punto borroso? Esa pregunta fue respondida inicialmente por Ernst Abbe en 1873. Teorizó que si dos objetos están más cerca de la mitad de la longitud de onda, no se pueden resolver. Abbe obtuvo su límite al considerar cómo la difracción de una lente difuminaría una fuente puntual.
Durante aproximadamente un siglo, El límite de difracción de Abbe se tomó como una verdad científica. Seguro, podría jugar algunos juegos con la luz de iluminación y el medio de imagen para obtener un factor de dos o tres, pero los factores de diez o 100 eran inconcebibles. Eso ha cambiado ahora con muchas técnicas de imágenes capaces de resolver más allá del límite de difracción de Abbe, que ahora yace destrozado en la esquina del taller de ciencia bajo la sombra de dos premios Nobel. ¿Pero todavía hay un límite? ¿Qué tan cerca pueden estar dos objetos antes de que se conviertan en un solo punto? Ésta es la pregunta que Evgenii Narimanov de la Universidad de Purdue ha tratado de responder en un reciente Fotónica avanzada papel.
Eliminación de imágenes borrosas
Cuando se trata de imágenes, Es mucho más sencillo dejar de lado el concepto de difracción y pensar en la información. Cuando se crea una imagen de un objeto, la luz es dispersada por el objeto hacia el sistema de imágenes. El patrón espacial, o información, de la imagen es transportada por las frecuencias espaciales de la luz. Para recuperar una imagen precisa, el sistema de imágenes debe transmitir esas frecuencias espaciales sin modificarlas. Pero, cada sistema tiene sus límites, por lo que se perderá la contribución de algunas frecuencias espaciales.
La imagen resultante se crea recombinando las frecuencias espaciales que son transmitidas por el sistema de imágenes. Si el sistema de imágenes no puede transmitir frecuencias por encima de un cierto límite, entonces la imagen no contendrá esa información, resultando en borrosidad. Si considera que el sistema de imágenes puede transmitir frecuencias espaciales hasta una frecuencia de corte, pero incapaz de transmitir frecuencias por encima del límite, entonces la resolución de la imagen resultante será exactamente la predicha por Abbe (pero con matemáticas más simples).
En efecto, la información transmitida por un sistema de imágenes se describe exactamente con las mismas matemáticas que utilizan los ingenieros que estudian la transmisión de datos a través de cables telefónicos, que permite utilizar las herramientas de la teoría de la información para predecir el rendimiento de los sistemas de imágenes.
Decodificando los mensajes en una imagen
Narimanov ha ido un paso más allá al abstraer el proceso de obtención de imágenes al considerar solo la transferencia de información, independientemente de cómo esté codificada esa información. Cuando eso esté hecho, la resolución de una imagen está determinada únicamente por la información mutua compartida entre el objeto y la imagen. En este marco, que es independiente de todos los detalles funcionales, el límite de resolución viene dado por el ruido introducido durante la transferencia de información. En la práctica, el ruido se debe al detector, dispersión de la luz, fluctuaciones en las condiciones de iluminación, y muchos más detalles.
Al adoptar este enfoque abstracto, Narimanov pudo producir una teoría que predice la mejor resolución posible para una imagen basándose únicamente en la relación entre la fuerza de la señal y la cantidad de ruido. Cuanto mayor sea la relación señal / ruido, cuanto mejor sea la resolución posible.
Aprovechando esta teoría, el documento también incluye una serie de cálculos para sistemas de imágenes más específicos, como los que utilizan iluminación estructurada, y para el caso de imágenes de objetos dispersos, que tienen pocas características a menudo agrupadas. También se discuten las posibilidades de mejorar una imagen con posprocesamiento:todos estamos familiarizados con los dramas de crímenes televisivos que parecen capaces de realzar las imágenes a voluntad. Aunque esto no es posible como se muestra en la televisión, hay un elemento de verdad. Los métodos válidos para el posprocesamiento computacional de una imagen pueden revelar algunos detalles ocultos. Esta teoría muestra los límites de ese enfoque, también.
El enfoque de Narimanov no revela qué aspecto de un sistema limita actualmente la resolución. Para eso, todavía se requieren modelos más específicos. En lugar de, Es mejor pensar en el modelo de Narimanov como una guía:¿dónde se encuentran las mayores ganancias en resolución con el menor esfuerzo? Esa información es útil para decidir dónde invertir tiempo y dinero.