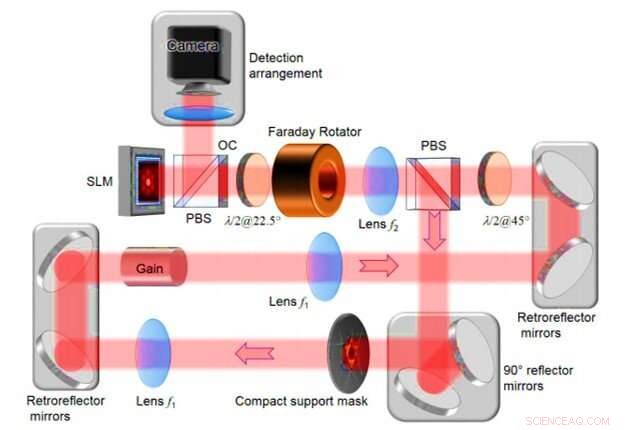
Disposición láser de cavidad degenerada de anillo digital experimental detallada. SLM - modulador espacial de luz; PBS - divisor de haz polarizador; λ/2@22,5 ° - placa de media onda con orientación angular de 22,5 °; λ / 2 @ 45 ° - placa de media onda con orientación angular de 45 °; máscara de soporte compacta - apertura intracavitaria en el plano de Fourier; Acoplador de salida OC. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
Los físicos pueden explorar sistemas físicos personalizados para resolver rápidamente tareas computacionales desafiantes mediante el desarrollo de simuladores de espín. optimización combinatoria y enfoque de la luz a través de medios de dispersión. En un nuevo informe sobre Avances de la ciencia , C. Tradonsky y un grupo de investigadores de los Departamentos de Física de Israel e India abordaron el problema de la recuperación de fases reconstruyendo un objeto a partir de su distribución de intensidad dispersa. El proceso experimental abordó un problema existente en disciplinas que van desde las imágenes de rayos X hasta la astrofísica que carecen de técnicas para reconstruir un objeto de interés, donde los científicos suelen utilizar algoritmos iterativos indirectos que son inherentemente lentos.
En el nuevo enfoque óptico, Tradonsky et al, por el contrario, utilizaron un modo láser de cavidad degenerada digital (DDCL) para reconstruir rápida y eficazmente el objeto de interés. Los resultados experimentales sugirieron que la competencia de ganancia entre los muchos modos láser actuó como una computadora altamente paralela para disolver rápidamente el problema de recuperación de fase. El enfoque se aplica a objetos bidimensionales (2-D) con soporte compacto conocido y objetos de valor complejo, para generalizar las imágenes a través de medios de dispersión, mientras realiza otras tareas computacionales desafiantes.
Para calcular la distribución de intensidad de la luz dispersa lejos de un objeto desconocido con relativa facilidad, los investigadores pueden calcular la fuente del valor absoluto de la transformada de Fourier de un objeto. La reconstrucción de un objeto a partir de su distribución de intensidad dispersa es, sin embargo, mal planteado ya que la información de fase se puede perder y diversas distribuciones de fase en el trabajo pueden resultar en diferentes reconstrucciones. Por tanto, los científicos deben obtener información previa sobre la forma de un objeto, positividad simetría espacial o escasez para reconstrucciones de objetos más precisas. Tales ejemplos se encuentran en astronomía, estudios de caracterización de pulsos cortos, Difracción de rayos X, detección de radar, reconocimiento de voz y al realizar imágenes en medios turbios. Durante la reconstrucción de objetos con una extensión finita (soporte compacto), los investigadores ofrecen una solución única al problema de recuperación de fase, siempre que modelen la misma intensidad dispersa con una resolución suficientemente alta.
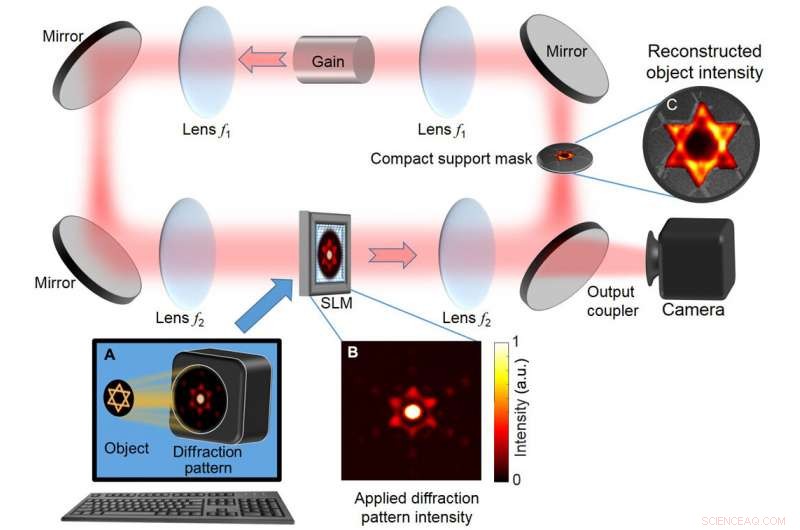
Disposición básica de DDCL para recuperación de fase rápida. (A) La distribución de intensidad dispersa calculada del objeto (esencialmente la distribución de intensidad de Fourier) se aplica a un SLM, que está incorporado en un láser de cavidad degenerada en anillo que puede soportar hasta 100, 000 modos transversales degenerados. Una máscara con la forma de los límites del objeto (soporte compacto) en el plano de Fourier filtra los modos extraños que no coinciden con el soporte compacto. Con esta disposición láser, el proceso de láser produce una solución autoconsistente que satisface tanto la distribución de intensidad dispersa que se muestra en (B) como la restricción del soporte compacto. (C) La intensidad del objeto reconstruido aparece en la máscara de soporte compacto y se refleja en la cámara. a.u., unidades arbitrarias. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
Los físicos habían desarrollado varios algoritmos para resolver el problema de recuperación de fase en la última década, incluido el algoritmo de reducción de errores de Gerchberg-Saxton (GS), algoritmo híbrido de entrada-entrada y reflexiones alternas promediadas relajadas (RAAR). Sin embargo, se basan en proyecciones iterativas que son relativamente lentas incluso en computadoras de alto rendimiento. Como alternativa, Los equipos de investigación pueden abordar los desafíos computacionales utilizando sistemas físicos diseñados específicamente. Si bien tales sistemas no son máquinas de Turing universales (es decir, no pueden realizar cálculos arbitrarios), potencialmente pueden resolver una clase específica de problemas de manera eficiente. Resolver problemas difíciles con tales sistemas puede resultar ventajoso en comparación con el uso de computadoras convencionales.
Tradonsky et al demostraron experimentalmente un nuevo sistema óptico para resolver rápidamente problemas de recuperación de fase basado en un láser de cavidad degenerada digital (DDCL). El dispositivo incorporó dos restricciones, incluidas las magnitudes de Fourier de la luz dispersa de un objeto y el soporte compacto. El proceso de láser no lineal dentro de la cavidad dio como resultado una solución autoconsistente que satisfizo ambas limitaciones. El mecanismo físico subyacente en el DDCL fue similar al observado con los estimuladores de espín del oscilador paramétrico óptico (OPO).
Tanto los simuladores OPO como los DDCL han realizado optimizaciones a través de una operación extremadamente rápida con la capacidad de evitar mínimos locales y poseían un paquete de ondas no gaussianas. Los científicos facilitaron la apertura del soporte compacto dentro de la cavidad para garantizar que las diferentes configuraciones de las fases del láser produzcan diferentes pérdidas. para permitir la configuración con pérdidas mínimas para ganar la competencia de modo y resolver el problema de fase. El sistema DDCL contenía muchas características atractivas e importantes, incluido un alto paralelismo para proporcionar millones de realizaciones experimentales paralelas, tiempos cortos de ida y vuelta de aproximadamente 20 nanosegundos, tiempos de convergencia rápidos y un modo de selección inherente que representó una pérdida mínima debido a la competencia de modo. En teoria, de todas las configuraciones de fase que evolucionan en el tiempo, el que tenía la energía más alta ganó la competencia de modo en relación con la ganancia limitada. Como resultado, mayor el número de configuraciones independientes iniciales en la práctica, mayor es la probabilidad del sistema de encontrar una solución correcta con una configuración estable y sin pérdidas.
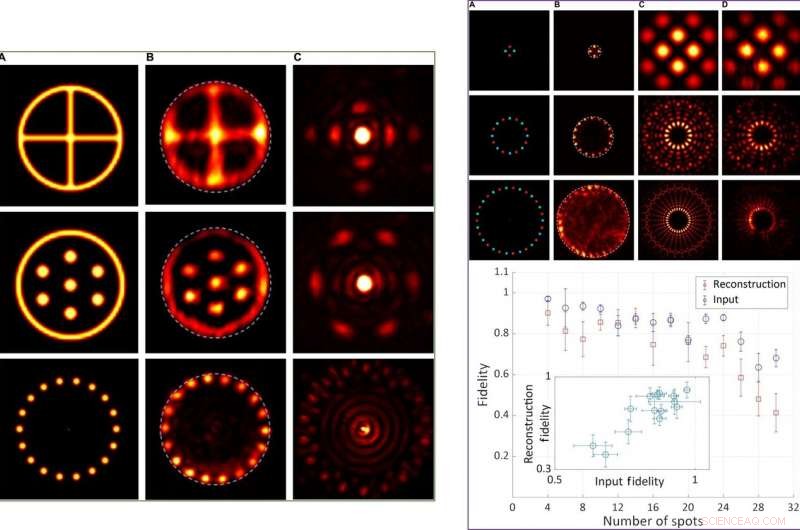
IZQUIERDA:Resultados experimentales para objetos centrosimétricos de valor real. Columna (A) Distribuciones de intensidad de los objetos reales. Columna (B) Distribución de intensidad detectada de los objetos reconstruidos, utilizando una apertura circular como soporte compacto. Columna (C) Distribuciones de intensidad de Fourier en el SLM. DERECHA:Resultados experimentales y cuantitativos de fidelidad en función de la complejidad del objeto. Arriba:Distribuciones de intensidad representativas de objetos con 4, dieciséis, y 30 plazas. Columna (A) Distribuciones de intensidad (brillo) y fase (tono) de los objetos reales. Columna (B) Distribución de intensidad detectada de los objetos reconstruidos, utilizando una apertura circular como soporte compacto. Columna (C) Distribuciones de intensidad de Fourier calculadas aplicadas para controlar el SLM. Columna (D) Se detectaron las distribuciones de intensidad de Fourier correspondientes después de modificaciones de las propiedades de SLM. Abajo:Valores de fidelidad cuantitativos de las distribuciones de intensidad de Fourier (azul) y las distribuciones de intensidad del objeto reconstruido (rojo) en función del número de puntos en el objeto (4 a 30). Recuadro:valores de fidelidad de las distribuciones de intensidad del objeto reconstruido en función de los valores de fidelidad de las distribuciones de intensidad de Fourier para todas las mediciones. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530.
En la configuración experimental, Tradonsky et al incluyeron un láser de cavidad degenerada en anillo con un medio de ganancia inherente, dos telescopios 4f y un modulador de luz espacial de amplitud (SLM). El sistema también incluía una apertura intracavitaria, Espejos de reflectividad 3D y un acoplador de salida. El equipo usó los telescopios 4f izquierdos para obtener imágenes del centro del medio de ganancia en el SLM y controló la transmisión en cada píxel. independientemente. Combinaron la apertura intracavitaria con el SLM para controlar y formar la distribución de la intensidad del láser de salida. Cuando los científicos colocaron una abertura intracavitaria (máscara de soporte compacta) en el plano de Fourier entre las dos lentes, cada distribución de fase demostró un nivel diferente de pérdida. Como consecuencia, la distribución de fase con pérdida mínima fue el modo láser más probable en el estudio. El equipo consideró dos cifras de mérito para cuantificar la calidad del sistema, incluida la fidelidad de la solución y el tiempo de cálculo. El equipo de investigación obtuvo resultados representativos para objetos centrosimétricos con muy buena concordancia entre las distribuciones de intensidad del original (objeto real) y las formas reconstruidas.
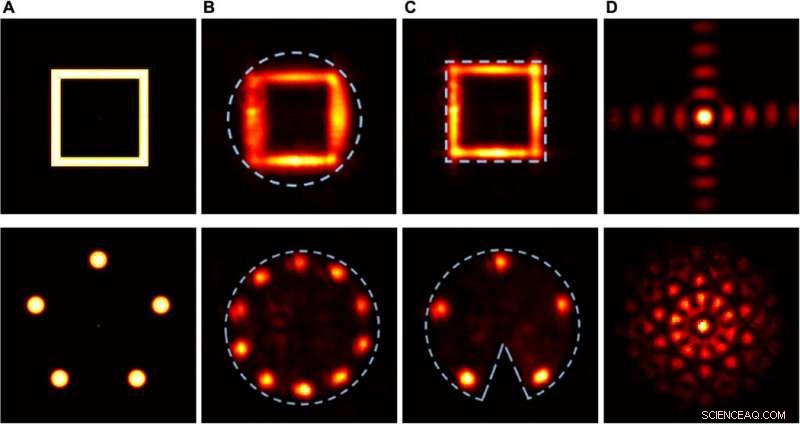
Resultados experimentales que demuestran el efecto cualitativo de estanqueidad y asimetría de soportes compactos. Columna (A) Distribución de intensidad de los objetos reales. Columna (B) Distribución de intensidad detectada de los objetos reconstruidos, utilizando una apertura circular como soporte compacto. Columna (C) Distribución de intensidad detectada de los objetos reconstruidos, utilizando una abertura cuadrada como soporte compacto apretado (fila superior) y una abertura circular con una cuña como soporte compacto asimétrico (fila inferior). Columna (D) Distribuciones de intensidad de Fourier en el SLM. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
Tradonsky et al midieron el efecto de la complejidad del objeto en la fidelidad de la reconstrucción y formaron distribuciones de intensidad representativas para objetos con cuatro, dieciséis, y 30 plazas. Los resultados mostraron que los objetos de mayor complejidad (aquellos con más puntos) mostraron una distribución de intensidad de Fourier de mayor complejidad, con intrincados detalles que no se pudieron resolver con el sistema actual. También notaron que las fidelidades de entrada y reconstrucción disminuyen con el aumento de la complejidad del objeto, lo que atribuyeron al ruido técnico fluctuante de la bomba láser. Llevaron a cabo experimentos cualitativos para evaluar el efecto de la rigidez y la simetría durante la reconstrucción de objetos. Los resultados mostraron que un soporte compacto apretado mejoró significativamente la calidad del objeto reconstruido.
Luego, el equipo investigó los efectos cuantitativos del radio de la apertura del soporte compacto sobre la calidad y fidelidad de la reconstrucción. Para objetos más grandes, la intensidad representativa sufrió un rápido decaimiento durante la fidelidad de la reconstrucción, ya que el láser no pudo soportar la forma del objeto. Con objetos más pequeños que la apertura del soporte compacto, Tradonsky et al observaron un deterioro más lento en la fidelidad. En total, observaron una reducción de la fidelidad de la reconstrucción cuando la cámara promedió entre múltiples realizaciones de un objeto dentro del sistema.
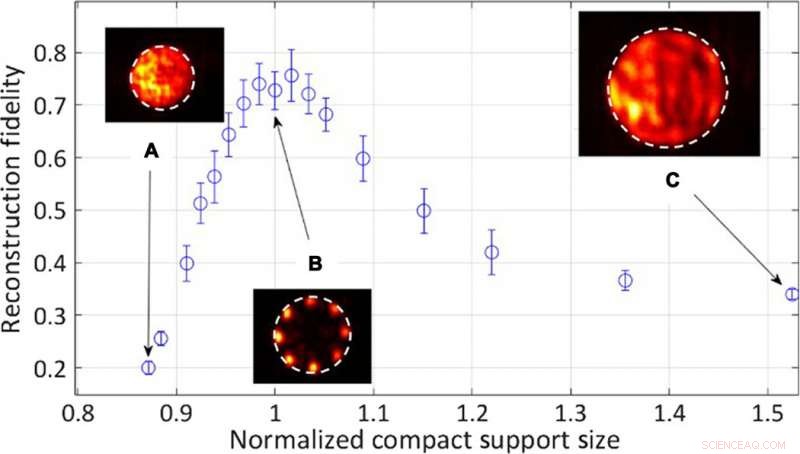
Resultados cuantitativos experimentales para la fidelidad de la reconstrucción en función del radio de apoyo compacto de la apertura normalizado por el tamaño del objeto. Recuadros:distribuciones típicas de intensidad de objetos reconstruidos. (A) El radio de soporte compacto es el 87% del radio del objeto. (B) El radio del objeto es igual al radio de soporte compacto. (C) El radio de soporte compacto es el 152% del radio del objeto. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530.
Generalmente, la resolución de los objetos reconstruidos fue relativamente baja debido a las aberraciones de fase en la cavidad del láser. El equipo propuso optimizar el sistema y reducir las aberraciones para mejorar la resolución. Los científicos también analizaron el tiempo necesario para ofrecer una solución de reconstrucción utilizando el sistema y encontraron que las duraciones dictadas por el SLM (modulador espacial de luz) y la lectura de la cámara eran de aproximadamente 20 ms. El tiempo real de cálculo del láser solo duró menos de 100 nanosegundos. Cuando Tradonsky et al optimizaron la configuración experimental utilizando una disposición de láser de cavidad degenerada lineal de conmutación Q con células pockel, redujeron el tiempo total de cálculo del sistema a aproximadamente 100 nanosegundos. Relativamente, el tiempo de reconstrucción con el algoritmo RAAR fue de un segundo.
De este modo. C. Tradonsky y sus colegas presentaron un sistema óptico para la recuperación de fase rápida utilizando un nuevo DDCL (láser digital de cavidad degenerada). El tiempo de cálculo ascendió a 100 nanosegundos; órdenes de magnitudes más rápidas que las convencionales, sistemas computacionales basados en algoritmos. Según los resultados, Varias modificaciones al sistema DDCL pueden mejorar potencialmente su rendimiento, incluida una mayor longitud de la cavidad láser para aumentar el número de investigaciones paralelas independientes. El equipo de investigación seguirá explorando el sistema para resolver una variedad de problemas y resolver la calidad de la imagen después de la propagación a través de medios de dispersión.
© 2019 Science X Network