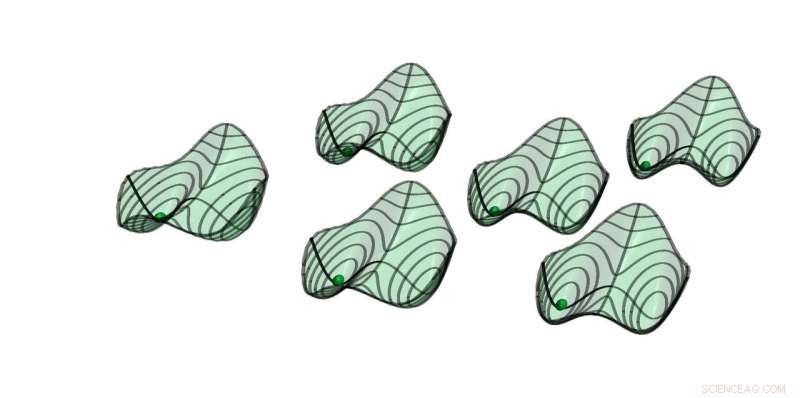
Cuasi potenciales de seis osciladores paramétricos con acoplamiento débil de todos a todos. Las soluciones estables se ubican en los mínimos. Las bolas indican la solución simétrica, donde todos los osciladores están en fase (captura de pantalla de la animación adjunta) Crédito:ETH Zurich / D-PHYS Toni Heugel
Estructuras conocidas como cristales de tiempo, que repiten en el tiempo la forma en que los cristales convencionales se repiten en el espacio, Recientemente han captado el interés y la imaginación de investigadores de todas las disciplinas. El concepto ha surgido del contexto de los sistemas cuánticos de muchos cuerpos, pero los físicos de ETH ahora han desarrollado un marco versátil que aclara las conexiones con obras clásicas que se remontan a casi dos siglos, proporcionando así una plataforma unificadora para explorar fenómenos aparentemente diferentes.
En un cristal los átomos están muy ordenados, ocupando ubicaciones bien definidas que forman patrones espaciales. Hace siete años, el premio Nobel de Física de 2004, Frank Wilczek, consideró la posibilidad de un análogo temporal del orden espacial cristalino:sistemas que muestran modulaciones temporales periódicas sostenidas en su estado de energía más baja. El concepto de tales estructuras con un estado fundamental oscilante es muy intrigante. Pobre de mí, poco después de que se publicara la idea, Se demostró que tales cristales de tiempo no son posibles sin romper las leyes fundamentales de la física. Sin embargo, El trabajo teórico posterior sugirió que cuando los sistemas cuánticos de muchos cuerpos son impulsados periódicamente, Surgen nuevas correlaciones de tiempo persistentes que evocan los cristales de tiempo de Wilczek. Estos sistemas impulsados se denominaron cristales de tiempo discreto, y en 2017, las primeras realizaciones experimentales de tales estados se informaron en conjuntos de partículas acopladas (iones, electrones y núcleos) que muestran propiedades mecánicas cuánticas.
Una historia no tan breve de los cristales de tiempo.
Pronto, observadores astutos detectaron distintas similitudes entre los cristales de tiempo discretos en los sistemas cuánticos y los llamados resonadores paramétricos, un concepto en la física clásica que se remonta al trabajo de Michael Faraday en 1831. La conexión entre estos dos cuerpos de trabajo permaneció, sin embargo, opaco. Ahora, Los teóricos han desarrollado un nuevo marco que contribuye en gran medida a eliminar las ambigüedades que rodean las similitudes entre los sistemas cuánticos y clásicos impulsados periódicamente.
Escribiendo en un artículo publicado hoy en la revista Cartas de revisión física , Toni Heugel, un doctorado estudiante del Departamento de Física de ETH Zurich, y Matthias Oscity, un estudiante de la misma institución, trabajando con el Dr. Ramasubramanian Chitra y el Prof. Oded Zilberberg del Instituto de Física Teórica y con el Dr. Alexander Eichler del Laboratorio de Física del Estado Sólido, Informar un trabajo teórico y experimental que establece cómo se pueden generar cristales de tiempo discretos que, Por un lado, no requieren efectos mecánicos cuánticos y, por otra parte, mostrar efectos genuinos de muchos cuerpos, que es una característica de los cristales de tiempo discretos reportados en sistemas cuánticos.
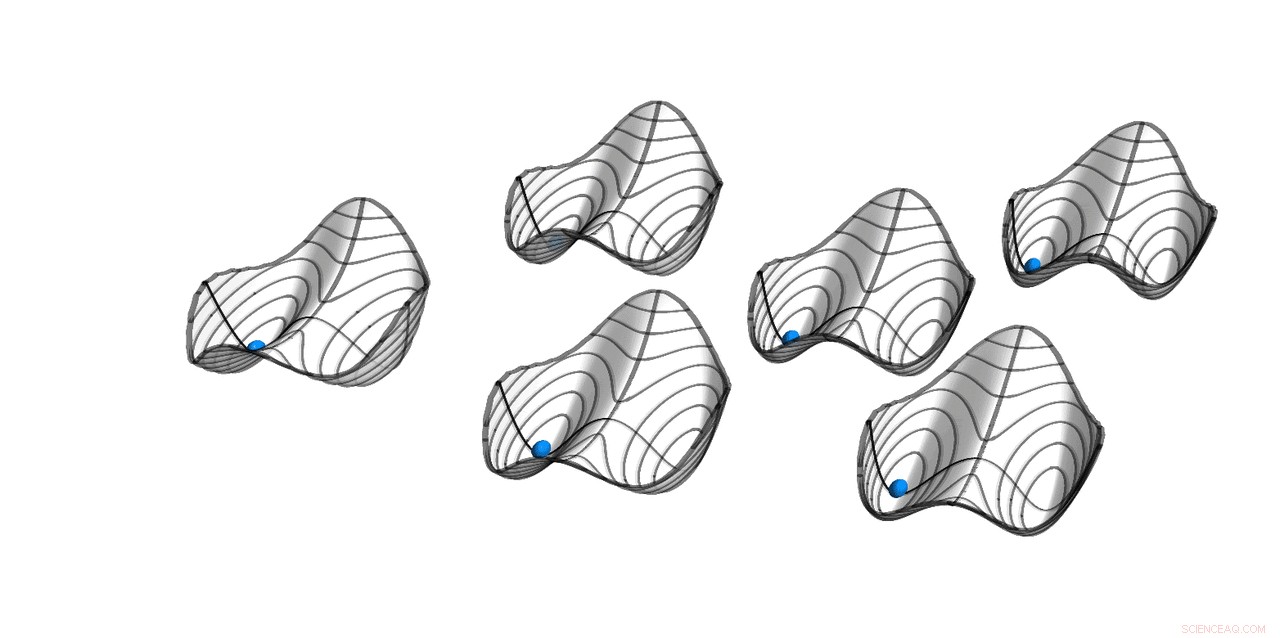
Cuasi potenciales de seis osciladores paramétricos con acoplamiento débil de todos a todos. Las soluciones estables se ubican en los mínimos. Las bolas indican la solución simétrica, donde todos los osciladores están en fase. El hamiltoniano H gobierna el movimiento del sistema tiene un período T, mientras que la solución en sí tiene un período 2T. Esta ruptura de la simetría de traslación de tiempo discreto hace que el sistema sea un cristal de tiempo discreto. Crédito:ETH Zurich / D-PHYS Toni Heugel
Muchas formas de frecuencias subarmónicas.
Existe una similitud obvia entre los resonadores paramétricos clásicos y los cristales de tiempo discreto realizados experimentalmente en sistemas cuánticos de muchos cuerpos:ambos muestran dinámicas emergentes en frecuencias que son fracciones de la frecuencia de excitación. En el contexto de cristales de tiempo discretos, la aparición de oscilaciones en tales frecuencias subarmónicas rompe la periodicidad temporal del sistema impulsado, proporcionar un 'tiempo análogo' al orden espacial cristalino, en el que se rompe la simetría del espacio. En los sistemas clásicos de accionamiento paramétrico, Las frecuencias subarmónicas aparecen de formas más familiares:un niño en un columpio, por ejemplo, modifica el centro de gravedad al doble de la frecuencia de la oscilación resultante, o la cola de caballo de un corredor oscila a la mitad de la frecuencia del movimiento vertical de la cabeza.
Pero, ¿estos fenómenos disímiles tienen algo que ver entre sí? Sí, dicen los físicos de ETH. En particular, señalan dónde aparecen los aspectos de muchos cuerpos en los sistemas clásicos. Para hacerlo consideraron osciladores no lineales clásicos con acoplamiento sintonizable entre ellos.
Marco unificador para sistemas clásicos y cuánticos impulsados periódicamente
Es bien sabido que para ciertas frecuencias de conducción y puntos fuertes, Los osciladores paramétricos se vuelven inestables y luego se someten a la llamada bifurcación de duplicación del período, más allá del cual oscilan a la mitad de su frecuencia de conducción. Heugel, Oscity y sus colegas exploran lo que sucede cuando varios de estos osciladores se acoplan. Tanto en cálculos como en experimentos que utilizan dos cadenas con acoplamiento variable entre ellas, encuentran dos regímenes distintos. Cuando el acoplamiento es fuerte, el sistema de dos cuerdas se mueve colectivamente, recreando en esencia los movimientos del niño en un columpio o la cola de caballo de un corredor. Sin embargo, en el caso de un acoplamiento débil entre las cuerdas, la dinámica de cada cuerda es similar a la mostrada por el sistema desacoplado. Como consecuencia, los osciladores acoplados no se bifurcan colectivamente sino que se bifurcan individualmente en parámetros ligeramente diferentes del variador, conduciendo a una dinámica general más rica, que se vuelven cada vez más complejos a medida que los sistemas se hacen más grandes.
Los investigadores de ETH argumentan que estos modos débilmente acoplados son similares a los que surgen en los sistemas cuánticos de muchos cuerpos. lo que implica que su marco podría explicar los comportamientos vistos experimentalmente en estos sistemas. Es más, el nuevo trabajo prescribe condiciones generales para generar cristales de tiempo clásicos de muchos cuerpos. En última instancia, estos podrían usarse tanto para interpretar como para explorar características de sus contrapartes cuánticas.
Tomados en conjunto, Por lo tanto, estos hallazgos proporcionan un poderoso marco unificador para sistemas clásicos y cuánticos impulsados periódicamente que muestran dinámicas en frecuencias subarmónicas emergentes, sistemas que hasta ahora se han descrito en contextos muy diferentes. pero puede que no sea tan diferente después de todo.