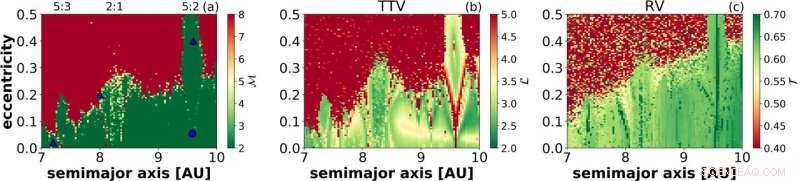
Un mapa de estabilidad de Saturno obtenido por el indicador de caos MEGNO (a) y la red de recurrencia mide la longitud promedio del camino (b) y la transitividad (c). Los dos últimos paneles se basan en la variación del tiempo de tránsito de Júpiter y la velocidad radial del sol, respectivamente. Crédito:Tamás Kovács
Los exoplanetas que giran alrededor de estrellas distantes se están enfocando rápidamente con tecnología avanzada como el telescopio espacial Kepler. Obtener una comprensión completa de esos sistemas es difícil, porque se desconocen las posiciones y velocidades iniciales de los exoplanetas. Determinar si la dinámica del sistema es cuasiperiódica o caótica es engorroso, caro y exigente computacionalmente.
En esta semana Caos , Tamás Kovács ofrece un método alternativo para el análisis de estabilidad de cuerpos exoplanetarios utilizando solo los datos de series de tiempo observadas para deducir medidas dinámicas y cuantificar la imprevisibilidad de los sistemas de exoplanetas.
"Si no conocemos las ecuaciones que gobiernan el movimiento de un sistema, y solo tenemos la serie de tiempo, lo que medimos con el telescopio, entonces queremos transformar esa serie de tiempo en una red compleja. En este caso, se llama red de recurrencia, ", Dijo Kovács." Esta red contiene todas las características dinámicas del sistema subyacente que queremos analizar ".
El documento se basa en el trabajo del físico Floris Takens, quien propuso en 1981 que la dinámica de un sistema podría reconstruirse utilizando una serie de observaciones sobre el estado del sistema. Con el teorema de incrustación de Takens como punto de partida, Kovács utiliza la incrustación de retardo de tiempo para reconstruir una trayectoria de alta dimensión y luego identificar puntos de recurrencia, donde los cuerpos en el espacio de fase están cerca unos de otros.
"Esos puntos especiales serán los vértices y los bordes de la red compleja, "Dijo Kovács." Una vez que tengas la red, puedes reprogramar esta red para poder aplicar medidas como la transitividad, longitud de ruta promedio u otras únicas para esa red ".
Kovács prueba la confiabilidad del método utilizando un sistema conocido como modelo, el sistema de tres cuerpos de Saturno, Júpiter y el sol y luego lo aplica al sistema Kepler 36b y 36c. Los resultados de su sistema Kepler concuerdan con lo que se conoce.
"Estudios anteriores señalaron que Kepler 36b y 36c es un sistema muy especial, porque a partir de la simulación directa y las integraciones numéricas, vemos que el sistema está al borde del caos, "Dijo Kovács." A veces, muestra una dinámica regular, y en otras ocasiones, parece ser caótico ".
El autor planea aplicar a continuación sus métodos a sistemas con más de tres cuerpos, probando su escalabilidad y explorando su capacidad para manejar series de tiempo más largas y conjuntos de datos más nítidos.