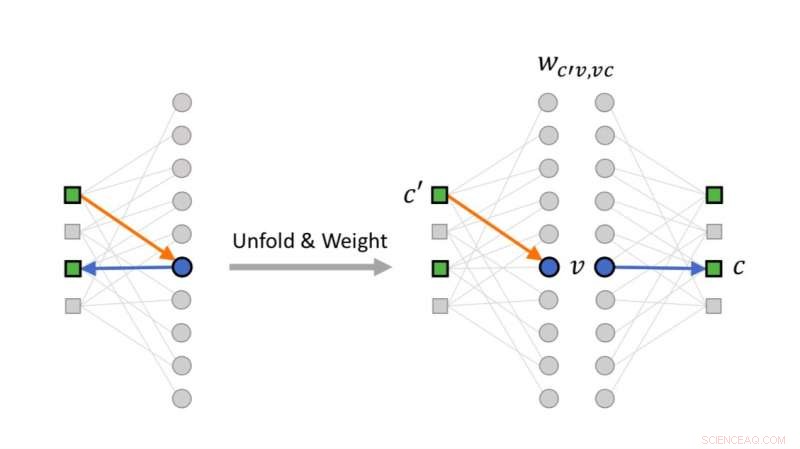
Propagación de creencias neuronales como transmisión de mensajes ponderados y desplegados. Crédito:Liu &Poulin.
Dos investigadores de la Université de Sherbrooke, en Canadá, Recientemente, han desarrollado y entrenado decodificadores de propagación de creencias neuronales (BP) para códigos cuánticos de verificación de paridad de baja densidad (LDPC). Su estudio, descrito en un artículo publicado en Physical Review Letters, sugiere que el entrenamiento puede mejorar significativamente el rendimiento de los decodificadores de BP, ayudando a resolver problemas que se asocian comúnmente con su aplicación en la investigación cuántica.
"Hace diez años, Escribí un artículo con Yeojin Chung explicando cómo los algoritmos de decodificación estándar para códigos LDPC, que se utilizan ampliamente en la comunicación clásica, fallaría en la configuración cuántica, "David Poulin, uno de los investigadores que realizó el estudio, dijo Phys.org. "Este problema me ha estado obsesionando desde entonces. Recientemente, la gente ha comenzado a investigar el uso de redes neuronales para decodificar códigos cuánticos, pero todos se enfocaron en un problema (decodificación de códigos topológicos) que ya tenía una serie de buenas soluciones diseñadas por humanos. Esta fue la ocasión perfecta para revisar mi problema abierto favorito y usar redes neuronales para decodificar códigos cuánticos que no tenían un decodificador conocido anteriormente ".
Si bien los decodificadores BP se aplican comúnmente en una variedad de configuraciones, hasta ahora han demostrado ser inadecuados para decodificar códigos cuánticos de corrección de errores. Esto se debe a una característica cuántica única conocida como 'degeneración de errores, "lo que esencialmente significa que hay varias formas de corregir un error en la configuración cuántica.
Los algoritmos clásicos de PA constan de tres ecuaciones simples. La estructura de estas ecuaciones permite un mapeo exacto a una red neuronal de retroalimentación. En otras palabras, Es posible reinterpretar las ecuaciones de BP comúnmente utilizadas para decodificar códigos LDPC como una descripción de la configuración inicial de una red neuronal.
Investigaciones anteriores han encontrado que esta 'red neuronal inicial' no funciona bien en entornos cuánticos, a pesar de lograr un mejor rendimiento que las redes neuronales aleatorias. En su estudio, Poulin y su colega Ye-Hua Liu mejoraron el rendimiento de la 'red neuronal inicial' entrenándola con datos generados por simulaciones numéricas.
"El entrenamiento está guiado por una función objetivo que tiene en cuenta los efectos cuánticos, "Liu le dijo a Phys.org." En términos generales, Los decodificadores neuronales tienen la ventaja de que se adaptan a estadísticas de ruido arbitrarias en canales realistas. Además de eso, nuestro método es aplicable a códigos LDPC cuánticos sin estructuras reticulares regulares. Estos códigos son muy prometedores para realizar una corrección de errores cuánticos de baja sobrecarga ".
Los investigadores encontraron que entrenar a los decodificadores neuronales de BP utilizando la técnica que adoptaron mejoró su rendimiento, para todas las familias de códigos LDPC que probaron. Es más, la técnica de entrenamiento que utilizaron podría ayudar a resolver el problema de degeneración que generalmente afecta a la decodificación de códigos LDPC cuánticos.
"El entrenamiento de la red neuronal de BP puede mejorar significativamente su rendimiento para la corrección de errores cuánticos, lo que significa que un algoritmo clásico se puede adaptar al entorno cuántico mediante métodos de aprendizaje profundo, ", Dijo Liu." Esto nos inspira a buscar otros ejemplos como este en la física cuántica, para revelar una conexión más amplia entre el aprendizaje profundo y las ciencias naturales. Por ejemplo, La propagación de creencias se usa ampliamente en muchas otras áreas de investigación, incluida la física estadística, lo que implica que la PA neuronal también podría beneficiar la investigación en física estadística cuántica ".
En su trabajo futuro, Poulin y Liu planean estudiar la PA neuronal en el contexto de la física estadística. Si está entrenado con la misma técnica, los investigadores esperan que BP, que también se conoce como el 'método de la cavidad' en este entorno particular, también mostrará un rendimiento mejorado en este contexto.
"Mas ampliamente, La propagación de creencias pertenece a la clase importante de algoritmos de paso de mensajes, que resulta estar estrechamente relacionado con las redes convolucionales de gráficos en la investigación de aprendizaje profundo, "Añadió Liu." Sería muy provechoso obtener información sobre estas estructuras desde el punto de vista de un físico ".
© 2019 Science X Network