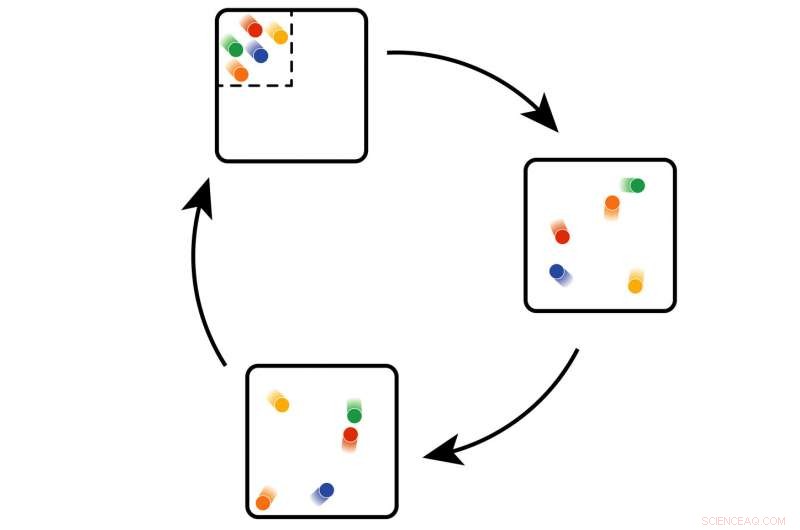
La recurrencia se puede demostrar con bolas en una caja:cuando comienzan en un estado ordenado, se volverán más desordenados. Pero en algún momento volverán al estado inicial; puede que tarde un poco. Crédito:TU Wien
Es uno de los resultados más asombrosos de la física:cuando un sistema complejo se deja solo, volverá a su estado inicial con una precisión casi perfecta. Partículas de gas, por ejemplo, girando caóticamente en un contenedor, volverán casi exactamente a sus posiciones iniciales después de un tiempo. El teorema de recurrencia de Poincaré es la base de la teoría del caos moderna. Por décadas, Los científicos han investigado cómo se puede aplicar este teorema al mundo de la física cuántica. Ahora, Los investigadores de TU Wien (Viena) han demostrado con éxito una especie de recurrencia de Poincaré en un sistema cuántico de múltiples partículas. Los resultados se han publicado en la revista Ciencias .
A finales del siglo XIX, el científico francés Henri Poincaré estudió sistemas que no pueden analizarse completamente con perfecta precisión, por ejemplo, sistemas solares que constan de muchos planetas y asteroides, o partículas de gas que chocan entre sí. Su sorprendente resultado:cada estado que es físicamente posible será ocupado por el sistema en algún momento, al menos en un muy buen grado de aproximación. Si esperamos lo suficiente en algún momento todos los planetas formarán una línea recta, solo por coincidencia. Las partículas de gas en una caja crearán patrones interesantes, o volver al estado en el que se encontraban cuando comenzó el experimento.
Se puede demostrar un teorema similar para los sistemas cuánticos. Allí, sin embargo, se aplican reglas completamente diferentes:"En física cuántica, tenemos que encontrar una forma completamente nueva de abordar este problema, "dice el profesor Jörg Schmiedmayer del Instituto de Física Atómica y Subatómica de TU Wien." Por razones muy fundamentales, el estado de un gran sistema cuántico, que consta de muchas partículas, nunca se puede medir perfectamente. Aparte de eso, las partículas no pueden verse como objetos independientes, tenemos que tener en cuenta que están entrelazados mecánicamente cuánticamente ".

El chip atómico utilizado para controlar nubes de átomos ultra fríos. Crédito:TU Wien
Ha habido intentos de demostrar el efecto de la "recurrencia de Poincaré" en sistemas cuánticos, pero hasta ahora esto solo ha sido posible con un número muy pequeño de partículas, cuyo estado se midió con la mayor precisión posible. Esto es extremadamente complicado y el tiempo que le toma al sistema volver a su estado original aumenta dramáticamente con el número de partículas. El equipo de Jörg Schmiedmayers en TU Wien, sin embargo, eligió un enfoque diferente:"No estamos tan interesados en el estado interno completo del sistema, que no se puede medir de todos modos, "dice Bernhard Rauer, primer autor de la publicación. "En su lugar, queremos preguntar:¿qué cantidades podemos observar, que nos dicen algo interesante sobre el sistema en su conjunto? ¿Y hay momentos en los que estas cantidades colectivas vuelven a su valor inicial? "
El equipo estudió el comportamiento de un gas ultrafrío, que consta de miles de átomos, que se mantiene en su lugar mediante campos electromagnéticos en un chip. "Hay varias cantidades diferentes que describen las características de tal gas cuántico, por ejemplo, longitudes de coherencia en el gas y funciones de correlación entre diferentes puntos en el espacio. Estos parámetros nos dicen:qué tan estrechamente están unidas las partículas por los efectos de la mecánica cuántica, "dice Sebastian Erne, quien fue el responsable de los cálculos teóricos necesarios para el proyecto. "Nuestra intuición diaria no está acostumbrada a lidiar con estas cantidades, pero para un sistema cuántico, son cruciales ".
Recurrencia descubierta, en cantidades colectivas
Midiendo tales cantidades, que no se refieren a partículas individuales, pero caracterizar el sistema en su conjunto, de hecho, era posible observar la recurrencia cuántica largamente buscada. Y no solo eso:"Con nuestro chip atómico, incluso podemos influir en el tiempo que tarda el sistema en volver a un estado en particular, ", dice Jörg Schmiedmayer." Al medir este tipo de recurrencia, aprendemos mucho sobre la dinámica colectiva de los átomos, por ejemplo, sobre la velocidad del sonido en el gas o sobre los fenómenos de dispersión de las ondas de densidad ".
La vieja pregunta si los sistemas cuánticos muestran recurrencias, finalmente se puede responder:Sí, lo hacen, pero el concepto de recurrencia tiene que redefinirse ligeramente. En lugar de intentar trazar el estado cuántico interno completo de un sistema, que no se puede medir de todos modos, tiene más sentido concentrarse en cantidades que pueden medirse en experimentos cuánticos. Se puede observar que estas cantidades se alejan de su valor inicial y, finalmente, regresan a su estado inicial.