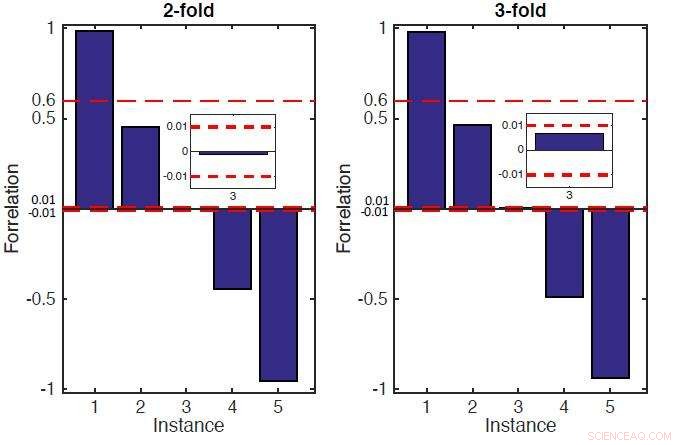
Se muestra el resultado de Forreation de 2 y 3 veces. Crédito:© Science China Press
Las funciones de correlación se emplean a menudo para cuantificar las relaciones entre variables o conjuntos de datos interdependientes. Hace unos pocos años, dos investigadores propusieron un problema de prueba de propiedades que involucraba Forrelation para estudiar la complejidad de las consultas de los dispositivos cuánticos. Ahora, Los científicos han realizado un estudio experimental de Forrelation en un procesador de información cuántica de resonancia magnética nuclear de 3 qubit.
El nuevo estudio fue publicado en Boletín de ciencia . Cuatro académicos de la Universidad de Tsinghua, Li Hang, Gao Xun, Xin Tao y Long Guilu, colaboró con un académico de la Universidad de Ciencia y Tecnología del Sur, Yung Man-Hong. En el estudio, Resolvieron problemas de Forrelation dobles y triples en espines nucleares y controlaron la fluctuación de espín dentro de un valor umbral utilizando un conjunto de secuencias de pulsos GRAPE optimizadas.
Se cree ampliamente que las computadoras cuánticas tienen una ventaja sobre las computadoras clásicas en muchos problemas computacionales. En el modelo de caja negra, muchos algoritmos cuánticos exhiben aceleraciones cuánticas. Esto plantea una pregunta:dentro del modelo de caja negra, ¿Qué tan grande es posible una aceleración cuántica? Específicamente, en la complejidad de las consultas, ¿Podemos encontrar la mayor separación entre las complejidades de las consultas clásicas y cuánticas?
Hace dos años, Aaronson y Ambainis introdujeron un nuevo problema de prueba de propiedades llamado Forrelation, que determina si una función booleana está altamente correlacionada con la transformada de Fourier de otra función booleana. Y demostraron que dio la mayor aceleración cuántica de caja negra hasta ahora conocida.
El profesor Long Guilu y sus colaboradores diseñaron un circuito cuántico para implementar Forrelations múltiples. Se dieron cuenta del caso doble y triple de Forrelations en un espectrómetro de resonancia magnética nuclear midiendo el valor de Forrelation para determinar si era mayor que 3/5 o el valor absoluto era menor que 1/100. Ésta es la primera realización experimental del problema Forrelation reportada en la literatura. Sus resultados se muestran en la figura 1.
Profesor Long Guilu, quien dirigió el experimento, dice, "Una de las dificultades es lograr una alta fidelidad de los estados finales, ya que el valor de Forrelation es muy sensible a la medición. Para controlar el error dentro de un valor umbral, utilizamos una técnica de ingeniería de pulsos de ascenso de gradiente optimizada en lugar de una secuencia de pulsos compuesta de pulsos duros y evoluciones de acoplamiento en J ".
El profesor Yung Man-Hong señala el futuro desarrollo de su trabajo:"Todos los algoritmos cuánticos se implementan en un procesador de información cuántica de tres qubit, que puede no presentar el poder de la computación cuántica sobre la computación clásica debido a las técnicas experimentales actuales. Sin embargo, este experimento prototipo indica que podemos ganar la supremacía cuántica en dispositivos cuánticos relativamente simples en un futuro próximo ".