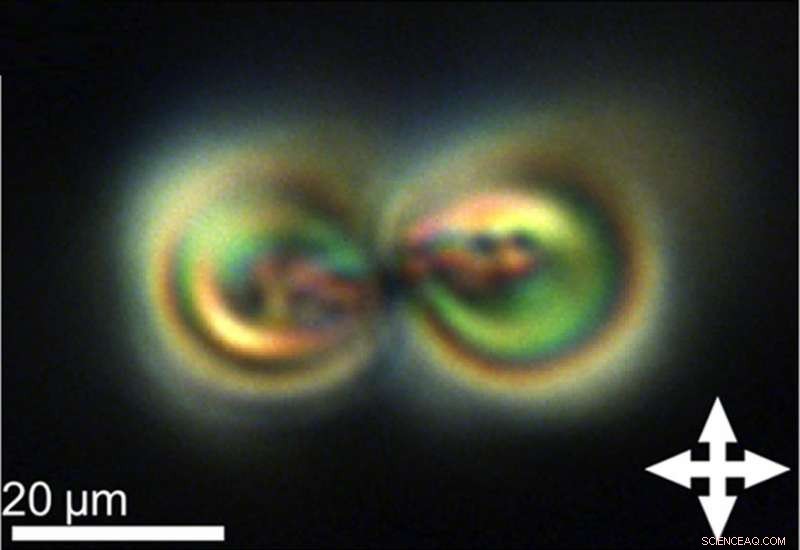
Una micrografía óptica polarizante de la torsión, un tipo de solitón topológico, observado en cristales líquidos nemáticos quirales. Crédito:Ackerman y Smalyukh. Publicado por la Sociedad Estadounidense de Física
(Phys.org) —Los físicos han descubierto que docenas de estructuras anudadas tridimensionales llamadas "solitones topológicos, "que han permanecido experimentalmente esquivas durante cientos de años, se puede crear y congelar durante largos períodos de tiempo en cristales líquidos como los que se utilizan en las pantallas electrónicas. Hasta ahora, Los solitones topológicos se han realizado solo en unos pocos experimentos, y durante tan poco tiempo que ha sido imposible estudiarlos con detalle.
Los nuevos resultados pueden cambiar todo eso, ya que proporcionan una forma de producir una amplia diversidad de solitones topológicos de larga duración que se pueden estudiar con microscopios y, quizas un dia, desempeñar un papel en nuevas aplicaciones ópticas y eléctricas.
Los investigadores, Paul J. Ackerman e Ivan I. Smalyukh en la Universidad de Colorado, Roca, han publicado un artículo sobre la realización experimental de solitones topológicos en un número reciente de Revisión física X .
"Nuestro trabajo establece enfoques experimentales y numéricos para estudios detallados de solitones topológicos 3-D, con la gran ventaja de permitir una comparación directa entre los resultados experimentales y teóricos y con un impacto potencial en muchas ramas de la física y el campo matemático de la topología, "Smalyukh dijo Phys.org . "Nuestro trabajo no solo demuestra experimentalmente los solitones topológicos 3-D que los matemáticos y físicos teóricos previeron anteriormente, pero también revela una serie de estructuras solitónicas que no se han anticipado ".
Fondo anudado
El interés por los solitones topológicos se remonta a principios del siglo XIX, cuando el matemático Carl Friedrich Gauss sugirió que las líneas de campos eléctricos y magnéticos forman nudos tridimensionales que podrían comportarse como partículas. Más tarde, Lord Kelvin y otros consideraron los vórtices anudados como un modelo temprano del átomo, en el que las propiedades de los nudos podrían explicar las propiedades químicas de los diferentes elementos.
En la actualidad, muchos modelos en física y cosmología involucran solitones topológicos, por ejemplo, modelos de sistemas de materia condensada, partículas elementales, monopolos magnéticos, y partículas magnéticas llamadas skyrmions que juegan un papel en el campo emergente de la espintrónica.
¿Qué son exactamente los solitones topológicos? Si toma dos o más anillos circulares, unirlos para hacer una cadena, luego distorsionar los anillos girando y tirando de ellos como si estuvieran hechos de masilla, y finalmente incrustar toda la estructura en una superficie de fondo, el resultado se vería como un solitón topológico. Describir estos objetos con más detalle requiere definirlos como objetos de cuatro dimensiones llamados "tres esferas, "y luego convertir estos objetos cuatridimensionales en objetos tridimensionales utilizando una técnica matemática llamada mapeo de Hopf. Son estos objetos tridimensionales, llamadas "preimágenes, "que son los anillos enlazados que se muestran en representaciones visuales.
Una de las razones por las que los solitones topológicos son tan difíciles de realizar experimentalmente es que corresponden al estado de energía más baja de un sistema físico para ser estable. Por esta razón, se han demostrado únicamente como estructuras transitorias en cristales líquidos. También es posible que existan solitones topológicos en otro medio, ferromagnetos quirales, pero la falta de técnicas de imágenes experimentales impide que los investigadores las observen.
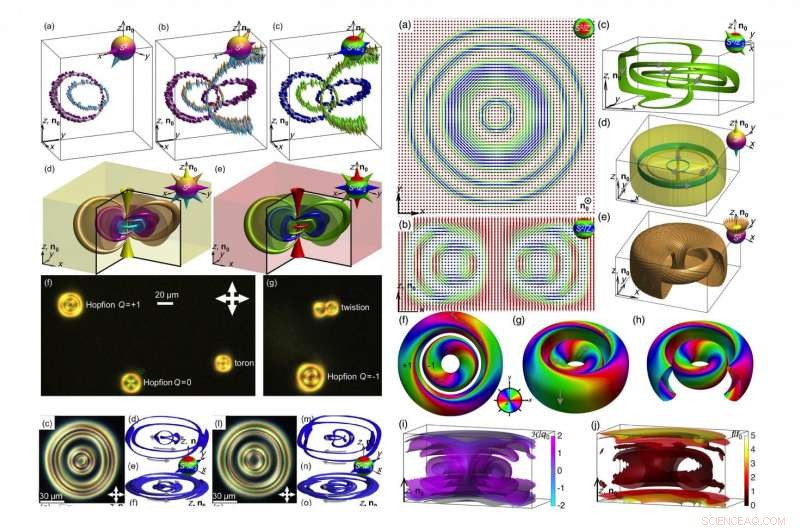
Una variedad de solitones topológicos, representado por simulaciones por computadora, ilustraciones de mapas de Hopf, y micrografías ópticas polarizantes. Crédito:Ackerman y Smalyukh. Publicado por la Sociedad Estadounidense de Física
Nudos de congelación
En el nuevo estudio, Los investigadores desarrollaron un método para "congelar" solitones topológicos en una película sólida de cristales líquidos nemáticos quirales a través de un proceso de polimerización que involucra niveles bajos de luz ultravioleta. junto con calefacción y refrigeración. Para permitir que el experimento sea ampliamente accesible, los investigadores utilizaron cristales líquidos disponibles comercialmente, a los que añadieron dopantes quirales. Usando pinzas ópticas para generar y manipular patrones en los cristales líquidos precongelados, los investigadores también pudieron controlar los tipos de solitones topológicos que se fabrican.
Después de que los solitones topológicos se congelen en los cristales líquidos, los investigadores pueden estudiarlos usando un microscopio óptico, específicamente, un microscopio polarizador de fluorescencia de excitación de tres fotones, que produce una señal óptica que se puede utilizar para construir imágenes tridimensionales de los solitones.
En la segunda parte de su estudio, los investigadores demostraron cómo estos datos podrían luego usarse para hacer simulaciones numéricas correspondientes a las estructuras físicas altamente complejas. Este proceso se basa en analizar los patrones de torsión energéticamente favorables que minimizan la energía libre elástica de los cristales líquidos. Esencialmente, este proceso de convertir las estructuras experimentales (preimágenes) en modelos numéricos es análogo al mapeo matemático de Hopf de objetos tridimensionales (preimágenes) en cuatro dimensiones.
Aplicaciones potenciales
La capacidad de generar solitones topológicos duraderos también abre las puertas a posibles aplicaciones. Una idea es aprovechar el hecho de que los diferentes solitones topológicos tienen propiedades ópticas distintas, que podría usarse en dispositivos ópticos que cambian la fase de la luz, así como en píxeles para pantallas ópticas. Además, si los solitones topológicos identificados aquí en cristales líquidos también existen en ferromagnetos sólidos, los investigadores esperan que potencialmente puedan revolucionar el campo de la skyrmionics, en el que los skyrmions podrían usarse para construir dispositivos magnéticos, como almacenamiento de datos y lógica.
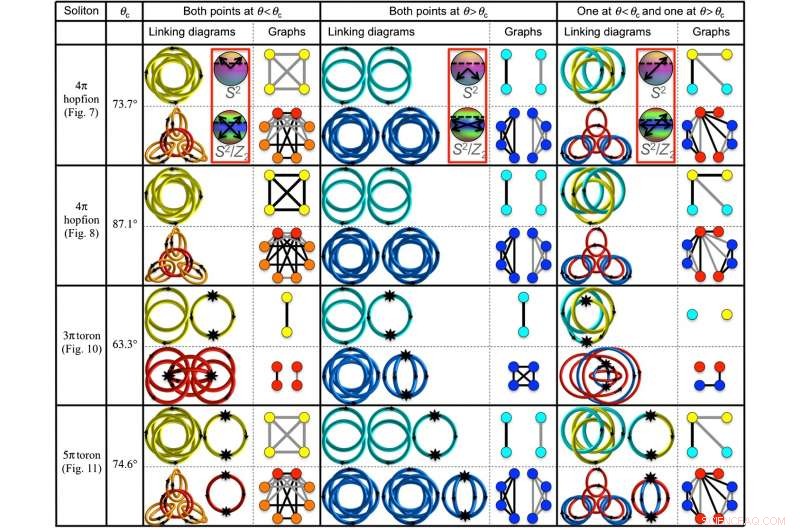
Vinculación de diagramas y gráficos de algunos solitones topológicos 3D. Crédito:Ackerman y Smalyukh. Publicado por la Sociedad Estadounidense de Física
"La gran variedad de solitones topológicos estables localizados a largo plazo, combinado con las propiedades electroópticas únicas del medio anfitrión de cristal líquido, conducirá inevitablemente a aplicaciones tecnológicas, como dispositivos electroópticos y pantallas de información biestables, ", Dijo Ackerman." También surge un amplio espectro de nuevas oportunidades en el aspecto fundamental, donde nuestro grupo de investigación trabajará para establecer cómo diferentes solitones topológicos pueden transformarse entre sí y también cómo los solitones con valores de índice de Hopf grandes pueden realizarse experimentalmente ".
En general, Una de las mayores ventajas del nuevo método es que proporciona un método mucho más completo, análisis detallado de preimágenes de solitones topológicos que otros métodos de construcción. Como resultado, el nuevo método descubre pequeños detalles en la topología que podrían pasarse por alto fácilmente de otra manera, como diferencias sutiles entre estructuras muy similares que podrían haberse confundido con la misma estructura. Los resultados muestran que los solitones topológicos son más complejos y diversos de lo que podría mostrar la evidencia anterior, e indican que muchas más de estas estructuras aún están a la espera de ser descubiertas.
"Puede existir una cantidad infinitamente grande de solitones topológicos, especialmente al considerar diferentes sistemas físicos, "Dijo Smalyukh.
© 2017 Phys.org