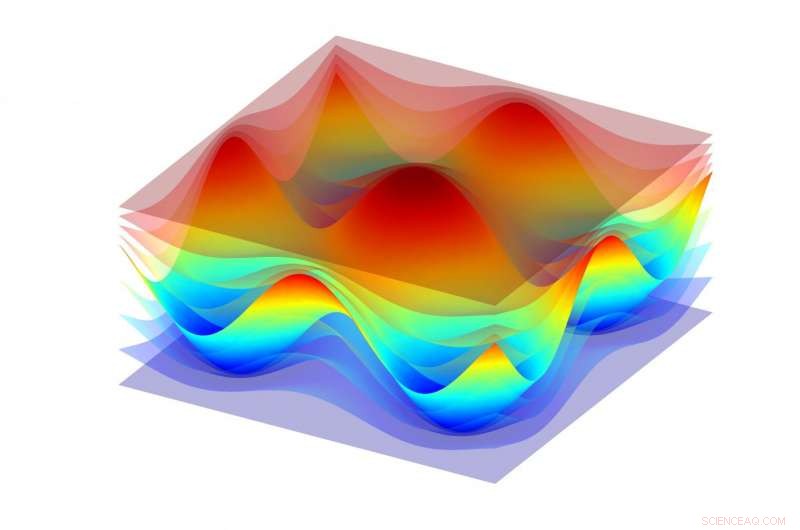
Planos de coordenadas de un sistema de coordenadas curvilíneas introducido en una región cercana a una rejilla de difracción sinusoidal bidimensional de modo que uno de los planos coincida con la superficie de la rejilla (una superficie opaca). Crédito:MIPT
Físicos del MIPT y de la Universidad Jean Monnet (Francia) han desarrollado un nuevo método de simulación para elementos ópticos que se utilizan en muchos instrumentos y dispositivos modernos. Su papel presentar una descripción del método que permite diseñar dispositivos ópticos complejos en tarjetas gráficas para juegos, ha sido publicado en el Revista de espectroscopia cuantitativa y transferencia radiativa .
Alexey Shcherbakov, un empleado del Laboratorio de Nanoóptica y Plasmónica en el Centro de Optoelectrónica a Nanoescala del MIPT, y su colega de la Universidad Jean Monnet Alexandre Tishchenko (1958-2016) propuso un nuevo enfoque para calcular los parámetros ópticos de las redes de difracción complejas y los elementos difractivos. Las posibilidades del método recientemente desarrollado son significativamente mayores que las que ofrecen otros métodos ampliamente utilizados para una variedad de estructuras ópticas. Los resultados del estudio abren nuevas perspectivas para la optimización altamente eficiente de dispositivos ópticos y optoelectrónicos modernos.
Las rejillas de difracción son elementos ópticos que forman la base de muchos dispositivos modernos en espectroscopia, telecomunicaciones y tecnologías láser. Son estructuras periódicas unidimensionales o bidimensionales que contienen miles de elementos regulares, por ejemplo, una serie de tiras paralelas de ancho microscópico. Las rejillas de difracción son capaces de dividir la luz blanca en un espectro, reflejando rayos de diferentes longitudes de onda en diferentes direcciones, por eso se utilizan en prácticamente todos los espectrómetros.
Un buen ejemplo de red de difracción es un disco compacto ordinario. Si está iluminado con luz de una frecuencia fija, un puntero láser rojo, por ejemplo, en lugar de un solo haz reflejado, aparece un conjunto de rayos reflejados. Estos se conocen como órdenes de difracción. Las direcciones en las que se propagan estos haces son fijas y dependen del período de rejilla (definido como la distancia entre elementos adyacentes), el ángulo de incidencia, y la frecuencia de radiación. Calculando la intensidad de cada orden de difracción, es decir., la cantidad de energía de la luz incidente que se refleja en cada dirección, es mucho más difícil. Realizar este tipo de cálculos con alta precisión es extremadamente importante desde un punto de vista práctico, ya que son vitales para la optimización de una amplia variedad de instrumentos y dispositivos.
La capacidad de las rejillas de difracción para dividir la luz en un espectro se utiliza en espectrómetros, dispositivos que utilizan el análisis del espectro para determinar la composición de varias sustancias, incluidas las soluciones químicas y los gases interestelares. La simulación de difracción es esencial para la fabricación de máscaras de litografía utilizadas en la fabricación microelectrónica moderna. y para diseñar polarizadores especiales en tecnología láser de procesamiento de metales. Además, Las estructuras periódicas se utilizan para aumentar la eficiencia de los concentradores solares y las células fotovoltaicas al aumentar la absorción de luz. Las estructuras periódicas también dificultan la falsificación de documentos y dinero:un patrón de finas tiras metálicas en el papel que reflejan la luz de cierta manera puede actuar como una contramedida contra la falsificación.
Un cálculo riguroso de la eficiencia del orden de difracción solo es posible resolviendo las ecuaciones de Maxwell:ecuaciones fundamentales que describen el campo electromagnético y, en particular, Propagación de ondas electromagnéticas. Fueron formulados hace más de cien años, pero una amplia variedad de soluciones que estas ecuaciones admiten en diferentes casos todavía motiva a muchos científicos de todo el mundo a seguir buscando nuevas soluciones. Y describir redes de difracción óptica complejas utilizando las ecuaciones de Maxwell solo es posible con la ayuda de métodos numéricos.

Alexey Shcherbakov demuestra el patrón de difracción de una rejilla bidimensional, crédito:Crédito:MIPT
Esto significa que en lugar de una fórmula lista para usar, debe implementarse un algoritmo de precisión finita. Para analizar y optimizar redes de difracción complejas, los investigadores utilizan computadoras modernas y grupos de computadoras. Todo un campo de la ciencia que combina la física matemática, análisis numérico, programación, y otras áreas se dedica a explorar cómo escribir programas de computadora y realizar estos cálculos de la manera más eficiente. El desarrollo de este campo está siendo impulsado por los avances en las tecnologías de fabricación de estructuras de difracción. Los dispositivos más precisos plantean requisitos cada vez más altos para los métodos de simulación a nivel de diseño.
En su publicación, los investigadores desarrollaron el método de fuente generalizada (GSM), redujo significativamente el consumo de recursos informáticos en comparación con otros métodos. La idea se basa en fuentes hipotéticas de radiación electromagnética que sustituyen la inhomogeneidad estructural.
Según Alexey Shcherbakov, investigador senior del Laboratorio de Nanoóptica, esta idea puede, con ciertas limitaciones, se ilustrará de la siguiente manera:"Supongamos que arrojamos piedras al centro de un estanque circular. Las ondas generadas por las piedras serán circulares y se extenderán desde el centro del estanque hasta la orilla del agua. Ahora preguntémonos:¿Qué forma tendrán las olas si un barco flota en algún lugar del estanque? Resulta que si sacamos el bote y tiramos muchas piedras pequeñas en el lugar donde estaba flotando, Estas pequeñas piedras se pueden elegir de forma que el número total de olas que generan y la piedra que arrojamos al centro sea la misma que si el barco todavía estuviera flotando en el estanque. Esta sustitución hipotética puede parecer que complica la tarea, pero, en la práctica, este principio permite a los científicos resolver de manera eficiente problemas muy complejos de propagación de ondas ".
La idea clave del nuevo método basado en GSM era utilizar transformaciones de coordenadas curvilíneas en la región de la red. Dentro de la justificación del método, una superficie de rejilla rugosa se estira a un plano, lo que hace que sea muy sencillo calcular la reflexión y la refracción de las ondas. Preservar los efectos físicos causados por la rugosidad requiere cambiar simultáneamente las propiedades del entorno cercano a la superficie de una determinada manera tras dicho estiramiento. Por lo tanto, en lugar de reflejarse en la superficie de la rejilla ondulada, las ondas parecen pasar a través de un espacio no homogéneo, lo que ralentiza su propagación de manera diferente en diferentes lugares. Esta técnica mejora significativamente los cálculos y obtiene resultados mucho más precisos en el mismo tiempo de cálculo.
Además del desarrollo analítico del nuevo enfoque con fuentes métricas, los investigadores también demostraron la posibilidad de una paralelización eficiente del método y la realización de simulaciones en tarjetas gráficas. Esto significa que es posible utilizar componentes producidos comercialmente con los que todos los jugadores están familiarizados para simular rejillas de difracción muy complejas. La potencia de cálculo de los chips gráficos ya es mayor que la potencia de los procesadores, razón por la cual las tarjetas gráficas se utilizan en muchos laboratorios de todo el mundo. En la investigación publicada, La comparación de simulaciones en tarjetas gráficas y procesadores ordinarios demostró que un chip gráfico es capaz de realizar la tarea decenas de veces más rápido.