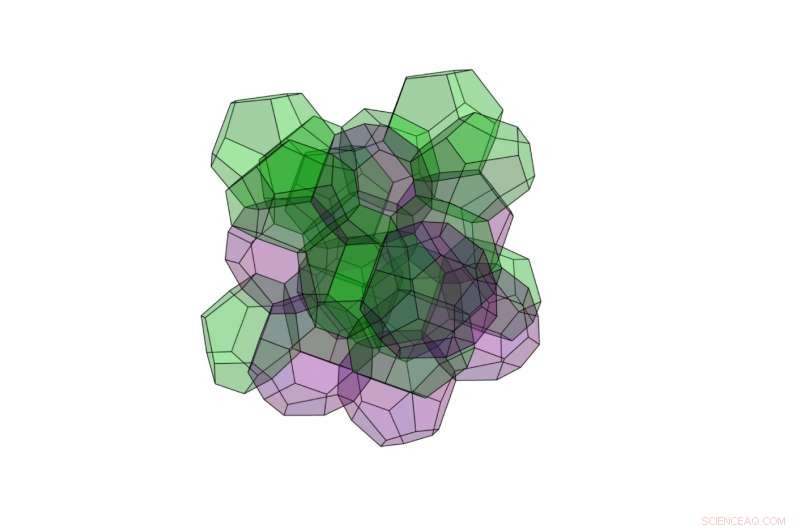
Una de las nuevas estructuras 3D tiene la superficie más baja de todas las estructuras de división del espacio conocidas:está hecha de 24 poliedros, algunos de los cuales tienen 12 caras y algunos de los cuales tienen 16 caras. Dado que los poliedros de 12 y 16 caras aquí tienen diferentes volúmenes, la nueva estructura no satisface el requisito original de Kelvin de volúmenes iguales. Crédito:Opsomer y Vandewalle. © 2016 IOP Publishing
(Phys.org) —Los investigadores han descubierto una nueva estructura 3D que divide el espacio en 24 regiones, y han demostrado que es la mejor solución hasta ahora para una versión modificada de un problema de división del espacio geométrico que ha desafiado a los investigadores durante más de un siglo.
En 1887, Lord Kelvin preguntó cómo se podría dividir el espacio en estructuras 3D de igual volumen de manera que se minimice el área de superficie total de cada estructura. Debe ser posible empaquetar firmemente muchas de estas estructuras juntas sin espacios entre ellas; en otras palabras, deben ser estructuras que "llenen el espacio". Cada estructura puede adoptar una variedad de formas 3D complejas, o "poliedros, "ya sea como un solo poliedro o una combinación de múltiples poliedros más pequeños de varios tipos. El desafío es averiguar qué tipos particulares de poliedros usar para minimizar el área de la superficie exterior de toda la estructura.
La mejor solución de Kelvin a este problema fue un solo poliedro llamado "tetrakaidecaedro, "que tiene 14 caras:seis cuadrados y ocho hexágonos. Dado que esta es la forma que se obtiene al cortar las esquinas de una forma de diamante 3D, también se puede pensar en un octaedro truncado.
Aunque la solución de Kelvin se mantuvo durante más de un siglo, en 1994, Denis Weaire y Robert Phelan del Trinity College de Dublín utilizaron simulaciones numéricas para descubrir una partición espacial más óptima. La solución de Weaire y Phelan está hecha de ocho poliedros de dos tipos diferentes, aunque ambos tipos tienen el mismo volumen:seis del tetracaidecaedro de Kelvin y dos del dodecaedro (que tiene 12 caras). Juntos, estos ocho poliedros forman una estructura 3D que tiene un 0,3% menos de superficie que el tetracaidecaedro único de Kelvin. La estructura de Weaire-Phelan se ha mantenido como la solución más óptima al problema de Kelvin durante los últimos 22 años.
Ahora en el nuevo estudio, Los físicos Eric Opsomer y Nicolas Vandewalle de la Universidad de Liége en Bélgica han desarrollado un nuevo algoritmo para encontrar estructuras poliédricas compuestas que llenan el espacio con una superficie mínima.
Usando el nuevo método, descubrieron que una nueva estructura 3D hecha de 24 poliedros tiene un área de superficie aún menor que la estructura de Weaire-Phelan. Los 24 poliedros son de dos tipos diferentes:algunos tienen 12 caras y algunos tienen 16 caras. A diferencia de la estructura de Weaire-Phelan, en el que los dos tipos diferentes de poliedros tienen volúmenes iguales, los poliedros de 12 y 16 caras aquí tienen volúmenes significativamente diferentes. Por esta razón, la nueva estructura no satisface el requisito original de Kelvin de volúmenes iguales.
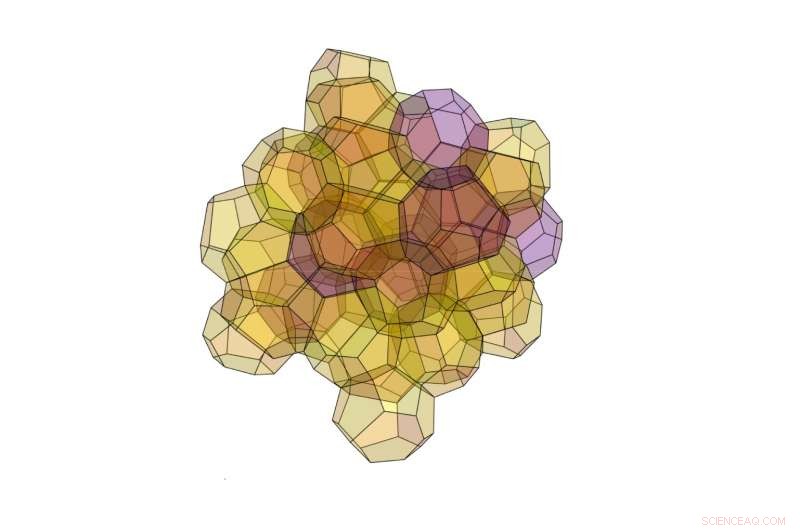
El nuevo algoritmo descubrió esta estructura 3D compuesta por 40 poliedros de dos tipos diferentes. Crédito:Opsomer y Vandewalle. © 2016 IOP Publishing
"Desafortunadamente, no es una 'verdadera solución, 'dado que las celdas de igual volumen son un requisito para el problema Kelvin original, "Opsomer dijo Phys.org . Sin embargo, la estructura sigue siendo interesante por otras razones. "Estos resultados pueden conducir al descubrimiento de estructuras con posibles implicaciones para la física de materiales, investigación médica, y otras áreas, "Dijo Opsomer.
Como explicaron los investigadores, eliminaron intencionalmente la restricción de volúmenes iguales al desarrollar su método de búsqueda porque les permitió diseñar el algoritmo de una manera nueva:en lugar de minimizar directamente el área de superficie de una estructura, maximizaron los isoperímetros promedio de los poliedros (los perímetros compartidos por todos los poliedros adyacentes). Si bien estos dos enfoques son diferentes, son, en última instancia, equivalentes.
Los investigadores utilizaron el nuevo algoritmo para explorar varias estructuras 3D hechas de entre dos y 64 poliedros. Comenzando con un número específico de puntos dispuestos aleatoriamente en el espacio 3D, el algoritmo comienza a mover los puntos. Después de cada iteración, el algoritmo calcula el nuevo isoperímetro promedio, y según el resultado, mantiene o rechaza la nueva configuración con una cierta probabilidad. Después de millones y, a veces, miles de millones de iteraciones, los puntos eventualmente forman los vértices de múltiples poliedros que juntos forman una estructura 3D con un área de superficie muy baja.
Como actualmente no hay forma de demostrar cuál es la estructura de partición de espacio más óptima (con o sin celdas de igual volumen), los investigadores planean continuar buscando una amplia variedad de estructuras de todo tipo. Su mejor conjetura es que existen estructuras aún más óptimas, y planean usar su algoritmo para continuar su exploración.
Los investigadores también esperan que el algoritmo pueda generar otras estructuras únicas. Una estructura particularmente interesante que descubrieron aquí es una estructura de 40 poliedros que es más óptima que la estructura de Kelvin, pero no tan buena como la estructura de Weaire-Phelan. Esta estructura altamente compleja también es inusual porque no pertenece a una categoría de estructuras llamadas estructuras de Frank-Kasper, en el que los investigadores se han centrado tradicionalmente para una partición óptima del espacio. El hallazgo sugiere que también pueden existir otras estructuras óptimas fuera de esta categoría.
Aunque el problema de Kelvin no se propuso originalmente para satisfacer ninguna necesidad práctica, La partición óptima del espacio ahora tiene una variedad de aplicaciones. En el campo de la medicina, estos conceptos se han utilizado para diseñar sólidos, reemplazos livianos de tejido óseo. La partición óptima del espacio también ha inspirado la arquitectura, con un ejemplo notable es el lugar de natación construido para los Juegos Olímpicos de Beijing 2008. El edificio, que se llama el cubo de agua, se basa en la estructura de Weaire-Phelan.
© 2016 Phys.org