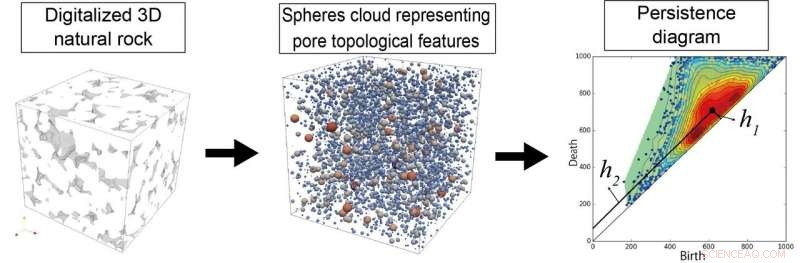
Figura:Izquierda:Esta es una roca natural 3D digitalizada, Centro:Nube de esferas que representan las características topológicas de los poros, Derecha:diagrama de persistencia. Crédito:Instituto Internacional de Investigación en Energía Neutral en Carbono (I2CNER) / Instituto de Matemáticas para la Industria (IMI), Universidad de Kyushu
Basado en la teoría de la homología persistente, Investigadores de la Universidad de Kyushu de Japón presentaron un nuevo parámetro y un nuevo método para evaluar la heterogeneidad de la porosidad.
Fukuoka, Japón:nos demos cuenta o no, las matemáticas impregnan nuestras vidas de innumerables formas. Algunas veces, el papel de las matemáticas es difícil de comprender, pero otras veces es sólido como una roca.
Aunque los granos minerales que forman una roca son importantes, son los poros, los espacios vacíos entre esos granos, los que a menudo transportan recursos vitales como el petróleo, gas, y agua potable. La geometría de los poros puede afectar fuertemente el almacenamiento, fluir, y extracción de esos recursos. Por lo tanto, Mejorar la comprensión de la geometría de los poros es de gran interés para muchos investigadores y profesionales de la industria.
En una fusión de matemáticas y ciencias de la tierra, Investigadores del Instituto Internacional para la Investigación de Energía Neutra en Carbono (I2CNER) y el Instituto de Matemáticas para la Industria (IMI) de la Universidad de Kyushu han desarrollado un método innovador para caracterizar la geometría de los poros. basado en un concepto llamado teoría de homología persistente, como se informa en un estudio publicado en Investigación de recursos hídricos .
Una diferencia importante entre las rocas naturales y los medios artificiales es que las características físicas de las rocas tienden a ser relativamente heterogéneas. Este método de última generación es particularmente útil para caracterizar esa heterogeneidad en los poros.
El primer autor del estudio, Fei Jiang, explica, "En el método propuesto, La geometría de poros compleja se transforma primero en datos de nubes esféricas. Luego, se calcula un diagrama de persistencia a partir de la nube de puntos. Un nuevo parámetro, el índice de distancia H como métrica, se deriva del diagrama de persistencia, y se propone caracterizar el grado de heterogeneidad de las rocas ".
Se confirmó una fuerte relación entre la heterogeneidad y el índice de distancia H. Además, Se propone una nueva ecuación empírica que utiliza esta métrica H para predecir el módulo de elasticidad efectivo de las rocas.
"Para probar el método propuesto recientemente basado en la geometría de rocas reales, cuatro tipos de rocas con diferentes estructuras de poros, incluyendo dos carbonatos y dos areniscas, fue investigado, "El coautor Takeshi Tsuji explica." El análisis del diagrama de persistencia fue más efectivo para estimar cuantitativamente la heterogeneidad de areniscas relativamente homogéneas en comparación con el método convencional. Este nuevo método también fue superior en términos de distinguir los diferentes tipos de rocas ".
Las ventajas adicionales de este método de análisis son que el diagrama de persistencia es relativamente estable con pequeños cambios en el espacio de los poros, y el índice de distancia H se puede calcular de manera muy eficiente. La información extraída del análisis del diagrama de persistencia se puede utilizar para predecir directamente las propiedades físicas (como la permeabilidad y la elasticidad) basadas en las microestructuras de las rocas. Por lo tanto, El análisis del diagrama de persistencia puede resultar una nueva herramienta importante para comprender la heterogeneidad de los poros en diferentes tipos de rocas.