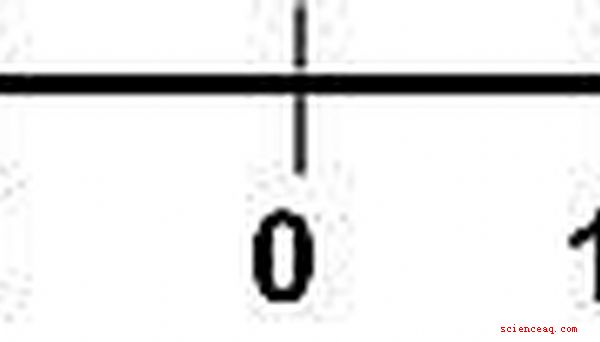
Una tarea común en matemáticas es calcular lo que se llama el valor absoluto de un número determinado. Normalmente utilizamos barras verticales alrededor del número para anotar esto, como se puede ver en la imagen. Leeríamos el lado izquierdo de la ecuación como "el valor absoluto de -4."
Las computadoras y las calculadoras a menudo usan el formato "abs (x)" en lugar de las barras verticales para representar el valor absoluto. Este artículo usará ese formato ya que eHow no permite el uso de la barra vertical en los artículos.
Lo que realmente nos preguntan es qué tan lejos está el número de cero en una recta numérica. Este es un tema extremadamente fácil, que generalmente se presenta en la escuela media, pero tiene aplicaciones más avanzadas en matemáticas de la escuela secundaria y la universidad.
Como se mencionó en la introducción, el valor absoluto de un número es su distancia desde cero en una recta numérica. Las distancias son siempre positivas sin importar en qué dirección vayamos. Nunca decimos que manejamos cinco millas negativas hacia la tienda.
El valor absoluto de un número es simplemente la versión positiva de un número. Si se nos pide que calculemos abs (5), simplemente tomamos nota del hecho de que 5 está a cinco unidades de 0 en una recta numérica. Decimos que abs (5) = 5. "El valor absoluto de 5 es 5."
Como otro ejemplo, si se nos pide que calculemos abs (-3), tomamos nota del hecho de que: 3 está a 3 unidades de 0. Pasa a estar a la izquierda de 0 en una recta numérica, pero todavía está a 3 unidades. Decimos que abs (-3) = 3. "El valor absoluto de -3 es 3." Si nuestro número original es negativo, solo respondemos con la versión positiva del número.
A veces los estudiantes se confunden y piensan que el valor absoluto nos dice que cambiemos el signo del número. Eso no es verdad. Mira la fórmula a la izquierda. Nos dice que si el número es positivo o 0, simplemente déjelo en blanco. Esa es la respuesta. Si es negativo, tu respuesta es el negativo de ese negativo, lo que lo hace positivo. Recuerde: la respuesta a un problema de valor absoluto siempre es positiva.
Eso es todo lo que hay en un nivel básico, y ciertamente en los grados inferiores esto es todo lo que se espera que los estudiantes sepan. A veces los estudiantes se molestan con esto, sintiendo que el asunto es una broma y un insulto a su inteligencia. Si bien la tarea presentada en este artículo es de hecho muy simple, el valor absoluto desempeña un papel importante en las matemáticas posteriores, y se utiliza de formas más complicadas.
Para proporcionar un poco de una vista previa, imagine que una máquina llena un botella de refresco, y otra máquina verifica que contenga entre 11.9 y 12.1 oz. de soda (para cumplir con la legalidad de etiquetarlo como 12 oz.) Si x es la cantidad real de onzas de refresco en la botella, entonces la máquina debe asegurarse de que abs (x - 12) < 0.1.
Eso realmente se ve peor de lo que es. Lo que estamos diciendo es que el peso del refresco no debe ser más de 0.1 oz. por encima o por debajo del objetivo de 12 oz Si está un poco apagado, no nos importa si es un poco más alto o más bajo. Todo lo que nos preocupa es que la magnitud del error es menor a 0.1. Ese es un ejemplo de una forma más avanzada en la que podemos usar el valor absoluto. De hecho, un problema que es muy similar a este ha aparecido en un antiguo examen SAT.
Por ahora, solo asegúrese de comprender la idea básica de cómo calcular un valor absoluto, para que gane tiene problemas cuando lo ve de nuevo en contextos más avanzados.