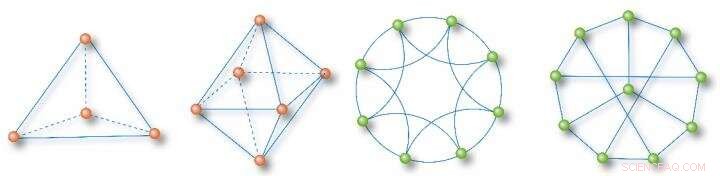
Ejemplos de redes totalmente homogéneas:un tetraedro, una red mínima de 2 cavidades, una red de vecino más cercano de 8 nodos, y una red de sincronización óptima de 10 nodos Crédito:Science China Press
Desde principios del siglo pasado, La investigación sobre sistemas complejos ha avanzado en los campos del caos, fractales y redes. Una red consta de nodos y bordes, donde los nodos representan los elementos de un sistema complejo y los bordes describen las interacciones entre ellos. Tales relaciones de borde de nodo pueden ser representadas por una matriz de adyacencia, cuyo orden es igual al número de nodos y cada suma de filas corresponde a un grado de nodo. La heterogeneidad de los grados de los nodos conduce a la aparición de estructuras en forma de estrella centradas en los nodos centrales.
Para abordar la heterogeneidad de los grados de los nodos, entró en juego el modelo de red sin escala, atrayendo una amplia atención. Hasta la fecha, a medida que avanza la tecnología de Internet y avanza la investigación de la red, Los investigadores se han dado cuenta de que la percepción tradicional sobre las redes heterogéneas basadas en estrellas es insuficiente para describir las redes complejas en evolución y los problemas científicos de las redes. Por ejemplo, Hay muchas comunidades en línea en Internet que dependen de estructuras sociales basadas en ciclos para la comunicación grupal y la difusión de información.
El funcionamiento de la red y las propiedades dinámicas tienen conexiones cada vez más estrechas con características topológicas de red de orden superior, subestructuras homogéneas e invariantes topológicos. Por lo tanto, Cambiar el enfoque de los grados de nodo a los números de ciclo revela muchas subredes totalmente homogéneas en redes complejas. Aquí, una red totalmente homogénea se define como una red con nodos que tienen el mismo grado, misma circunferencia (número de aristas en el ciclo más pequeño de un nodo), y la misma suma de rutas (suma de las rutas más cortas a un nodo desde todos los demás nodos). En la Figura 1 se muestran algunos ejemplos típicos a modo de ilustración.
A finales del siglo XIX, Poincaré descubrió que los límites son clave para diferenciar formas geométricas como discos, esferas y toros. Descompuso un objeto geométrico en componentes básicos llamados símplex (punto, línea, triángulo, tetraedro etc.), y luego introdujo los conceptos de agrupación por homología, Número de Betti y matriz de correlación de borde de nodo, y la fórmula de Euler-Poincaré, lo que muestra que la suma alternativa de simplesx es igual a la suma alternativa de números Betti.
La idea básica de Poincaré es dividir una forma geométrica compleja para simplificar el procedimiento de solución. Pudo hacerlo porque hay muchas subredes totalmente homogéneas, como triángulos y tetraedros (a los que se hace referencia como camarillas en la teoría de grafos o simplex en topología) en una red compleja. Son estructuras básicas para soportar funciones de red, a diferencia de las estrellas, son ciclos. Con estos elementos básicos, es posible describir una red usando una serie de espacios vectoriales sobre el campo binario.
Por ejemplo, el espacio vectorial tiene bordes como base, con dimensión igual al número de aristas; el espacio vectorial tiene triángulos como base, con dimensión igual al número de triángulos, etcétera. Dado que el límite de un triángulo consta de aristas, los dos espacios vectoriales adyacentes y se pueden correlacionar mediante un operador de límite, y su matriz de límites se puede utilizar para presentación y análisis. La matriz de límites tiene un contenido matemático más rico y es más útil que la matriz de adyacencia. Por ejemplo, utilizando el rango de la matriz de límites se puede calcular el número de Betti, un invariante importante de la red, que es el número de cavidades linealmente independientes de diferentes órdenes en la red, estableciendo un grupo de homología. La Figura 2 muestra las relaciones de algunos espacios vectoriales y sus correspondientes operadores de frontera.
En 2002, Xiaofan Wang y Guanrong Chen publicaron el primer criterio de sincronización de red. Le siguió una serie de trabajos que incluyeron la introducción de redes totalmente homogéneas a través de la optimización por parte de Dinghua Shi, Guanrong Chen y Xiaoyong Yan en 2013, revelando que la red totalmente homogénea con una circunferencia más larga y una ruta-suma más corta tiene una mejor sincronizabilidad entre redes del mismo tamaño. Además, en 2006, Linyuan Lü y Tao Zhou utilizaron el operador H para descubrir la relación entre el grado del nodo, Índice H y valor de kernel, estableciendo el teorema de DHC. En la investigación del índice de ciclo, un trabajo importante es el estudio empírico de Bassett et al. en 2018 en la red funcional del cerebro, en el que señalaron la importancia de las camarillas y cavidades en el funcionamiento de la red. Por último, si bien no menos importante, Recientemente descubrimos la estrecha relación de los números característicos de Euler con la sincronizabilidad de la red.
Esta serie de importantes resultados progresivos demuestra la importancia y la importancia de la investigación interdisciplinaria en física, biología y matemáticas. Teniendo en cuenta que esta nueva dirección del análisis estructural de redes que utiliza herramientas topológicas algebraicas es prometedora, los investigadores optaron por publicar su artículo actual, "Redes totalmente homogéneas, " en Revista Nacional de Ciencias .
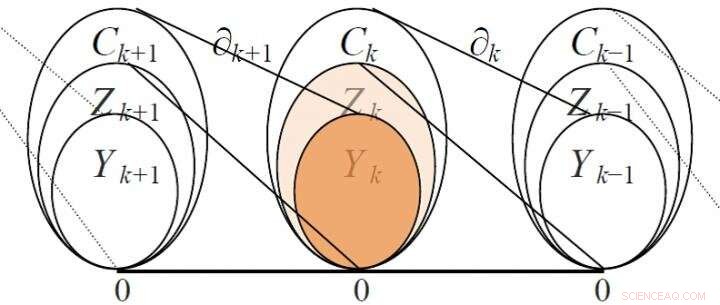
Relaciones de algunos espacios vectoriales y sus correspondientes operadores de frontera (Zk es un grupo cíclico, Yk es un grupo límite) Crédito:Science China Press