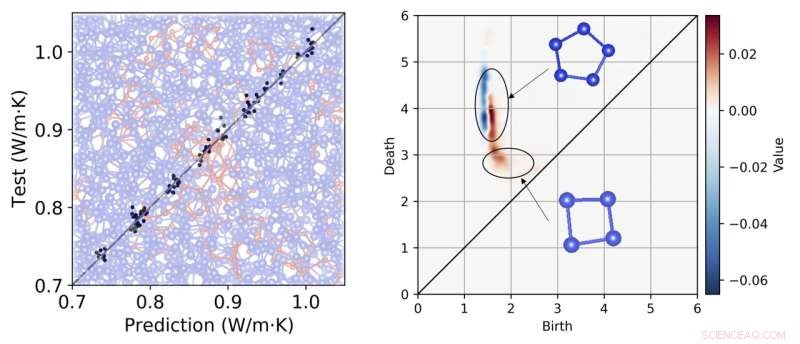
Izquierda:correlación entre los valores predichos por el análisis de homología persistente y los valores de prueba que fueron evaluados por simulaciones. Derecha:puntos de datos (regiones rojas y azules) en el diagrama persistente fuertemente correlacionados con los valores de conductividad térmica. Un ciclo de cinco vértices que se muestra en el diagrama es el componente mínimo del orden de rango medio, y un ciclo de cuatro vértices es el componente que rompe el orden de rango medio y reduce la conductividad térmica. Crédito:NINS/IMS
Los científicos teóricos han utilizado las matemáticas topológicas y el aprendizaje automático para identificar una relación oculta entre las estructuras a nanoescala y la conductividad térmica en el silicio amorfo, una forma vítrea del material sin un orden cristalino repetitivo.
Un estudio que describe su técnica apareció en el Journal of Chemical Physics .
Los sólidos amorfos, como el vidrio, la obsidiana, la cera y los plásticos, no tienen una estructura cristalina o repetitiva de largo alcance para los átomos o moléculas de los que están hechos. Esto contrasta con los sólidos cristalinos, como la sal, la mayoría de los metales y las rocas. Como carecen de un orden de largo alcance en su estructura, la conductividad térmica de los sólidos amorfos puede ser mucho menor que la de un sólido cristalino compuesto del mismo material.
Sin embargo, todavía puede haber algún orden de rango medio en la escala de nanómetros. Este orden de rango medio debería afectar la propagación y difusión de las vibraciones atómicas, que transportan calor. El transporte de calor en materiales desordenados es de especial interés para los físicos debido a su importancia en aplicaciones industriales. La forma amorfa de silicio se utiliza en una enorme variedad de aplicaciones en el mundo moderno, desde células solares hasta sensores de imagen. Por esta razón, los investigadores han investigado intensamente la firma estructural del orden de rango medio en el silicio amorfo y cómo se relaciona con la conductividad térmica.
"Para un mejor control sobre las aplicaciones que utilizan silicio amorfo, el control de sus propiedades térmicas ocupa un lugar destacado en la lista de deseos de los ingenieros", dijo Emi Minamitani, autor correspondiente del estudio y científico molecular teórico del Instituto de Ciencias Moleculares en Okazaki. Japón. "Extraer las características estructurales a escala nanométrica en forma amorfa, incluido el orden de rango medio, es una clave importante".
Desafortunadamente, los investigadores han tenido dificultades para llevar a cabo esta tarea porque es difícil determinar las características esenciales a escala nanométrica de los sistemas desordenados utilizando técnicas tradicionales.
En experimentos, la presencia de orden de rango medio se ha detectado físicamente mediante microscopía electrónica de fluctuación, que implica el análisis estadístico de la dispersión de volúmenes a escala nanométrica de un material desordenado. A nivel teórico, se ha discutido considerando la distribución de ángulos diédricos (el ángulo entre dos planos que se cruzan entre conjuntos de átomos) o usando "estadísticas de anillos". Este último trata de entender las características estructurales a partir de la conectividad de los átomos.
Esto, a su vez, se basa en el campo de las matemáticas conocido como topología, que investiga las propiedades de un objeto que no cambian, o son "invariantes", incluso cuando el objeto se estira y deforma constantemente sin romperse (como las formas escritas en una goma). sábana). Centrarse en esta invariancia topológica es útil para ofrecer una descripción cualitativa, como la tendencia de las propiedades físicas con respecto a la aleatoriedad. Sin embargo, es exigente determinar la estructura atómica correspondiente a un orden de rango medio y predecir sus propiedades físicas solo a partir de invariantes topológicos simples.
Entonces, los investigadores recurrieron a una técnica emergente llamada homología persistente, un tipo de análisis de datos topológicos. La homología persistente se ha utilizado en otros lugares para analizar estructuras complejas que van desde proteínas hasta sólidos amorfos. El beneficio de este método es detectar características topológicas en estructuras complicadas en diferentes escalas espaciales. Esto es vital porque el orden de rango medio comprende estructuras cuasi-repetitivas en varias escalas. Usando esta característica, podemos extraer el orden de rango medio oculto debajo de lo que de otro modo parecería aleatoriedad.
Los investigadores construyeron modelos computacionales de silicio amorfo mediante dinámica molecular clásica en los que la temperatura del silicio se incrementó por encima del punto de fusión y luego se enfrió gradualmente (enfriamiento) a temperatura ambiente. Se introdujeron diferencias en las características estructurales cambiando la velocidad de enfriamiento.
Luego, se calculó el diagrama persistente, que es la visualización bidimensional de la homología persistente, para cada modelo. Los investigadores se centraron en que los diagramas reflejaran las características estructurales del silicio amorfo. Por lo tanto, construyeron la representación numérica, llamada "descriptores", que podría usarse en el aprendizaje automático. El investigador descubrió que el diagrama persistente cumplió con la creación de un buen descriptor para usar en el procedimiento de aprendizaje automático, que a su vez logró predicciones precisas sobre las conductividades térmicas.
Al analizar más a fondo los datos de homología persistente y el modelo de aprendizaje automático, los investigadores ilustraron la relación previamente oculta entre el orden de rango medio en el silicio amorfo y su conductividad térmica.
El estudio ahora debería abrir una vía para controlar las características materiales del silicio amorfo y otros sólidos amorfos a través de la topología de sus nanoestructuras. Origen del pico del bosón en sólidos amorfos