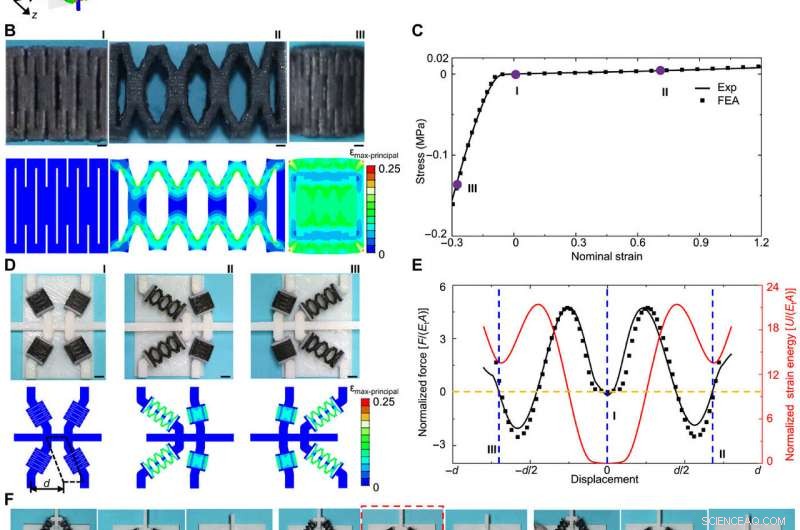
Conceptos de diseño y demostración de metamateriales mecánicos multiestables 2D con microestructuras kirigami en forma de X. (A) Ilustración esquemática de la construcción jerárquica de un metamaterial mecánico multiestable 2D, incluidas las celdas octogonales, Estructura de bloque de construcción en forma de X, y microestructuras de kirigami. (B) Imágenes ópticas y resultados FEA de las microestructuras kirigami en no deformadas, estirado, y estados comprimidos. (C) Curva nominal de tensión-deformación de la microestructura kirigami en (B), bajo tensión y compresión uniaxiales. (D) Imágenes ópticas y resultados FEA de las tres configuraciones estables diferentes de la estructura de bloques de construcción en forma de X impresa en 3D. (E) Dependencias de la fuerza normalizada y la energía de deformación normalizada en el desplazamiento horizontal aplicado a la estructura de bloques de construcción triestable en forma de X en (D). A denota el área de la sección transversal de la microestructura; Ec y Et denotan los módulos de compresión y tracción, respectivamente; d denota la distancia marcada en (D). (F) Demostración experimental de las configuraciones estables de una celda octagonal en el metamaterial mecánico. Las flechas rojas indican las direcciones en las que se mueven las barras de conexión horizontal y vertical. El estado intermedio en el que no se mueve ninguna barra de conexión está marcado por un marco punteado rojo. (G) Demostración experimental de cinco configuraciones estables representativas de un metamaterial mecánico impreso en 3D con los mismos parámetros geométricos que en (A). Barras de escala, 1 mm (B), 5 mm (D y F), y 25 mm (G). Créditos de las fotos:Hang Zhang, Universidad de Tsinghua. Crédito:Science Advances, doi:10.1126 / sciadv.abf1966
Los metamateriales mecánicos multiestables son materiales artificiales cuya microarquitectura ofrece más de dos configuraciones estables diferentes. Los metamateriales mecánicos existentes se basan en diseños basados en origami o kirigami con inestabilidad instantánea y mecanismos blandos microestructurados. Las estructuras escalables que se pueden construir a partir de metamateriales mecánicos con un número extremadamente grande de configuraciones estables programables siguen siendo difíciles de alcanzar. En un nuevo informe ahora publicado en Avances de la ciencia , Hang Zhang y un equipo de investigación en ingeniería, electrónica, y tecnología de estructura avanzada en Beijing, China, utilizó la asimetría elástica de tracción / compresión de las microestructuras kirigami para diseñar una clase de estructuras triestables en forma de X. El equipo usó estas construcciones como elementos de bloques de construcción para construir metamateriales mecánicos jerárquicos con geometrías cilíndricas unidimensionales, Celosías cuadradas 2D y celosías 3D cúbicas u octaédricas con multiestabilidad multidireccional. El número de estados estables aumentó con el número de células de metamateriales mecánicos incorporados en el trabajo, y las aplicaciones versátiles de multiestabilidad y diversidad estructural demostradas dentro de los operadores lógicos ternarios mecánicos con funcionalidades inusuales.
Metamateriales mecánicos
Los metamateriales mecánicos son un tipo de materiales artificiales que consisten en microestructuras periódicas con arquitecturas diseñadas para ofrecer propiedades mecánicas que superan a los materiales convencionales. A pesar de los avances en el campo, sigue siendo un desafío diseñar metamateriales jerárquicos con diversos estados estables y propiedades de estado estables adaptadas con precisión. En este trabajo, Zhang y col. introdujo una clase de microestructuras kirigami en forma de X como elementos de bloques de construcción triestables a partir de un esquema ascendente para lograr metamateriales mecánicos jerárquicos, con un mayor número de estados estables. La asimetría elástica de tracción-compresión de las microestructuras kirigami y la triestabilidad controlada independientemente de los metamateriales jerárquicos les permitió realizar vibraciones controladas de baja frecuencia a lo largo de diferentes direcciones en el plano para las funciones deseadas. incluida la supresión de ruido y la comunicación no lineal.
Metamateriales mecánicos multiestables con construcciones jerárquicas
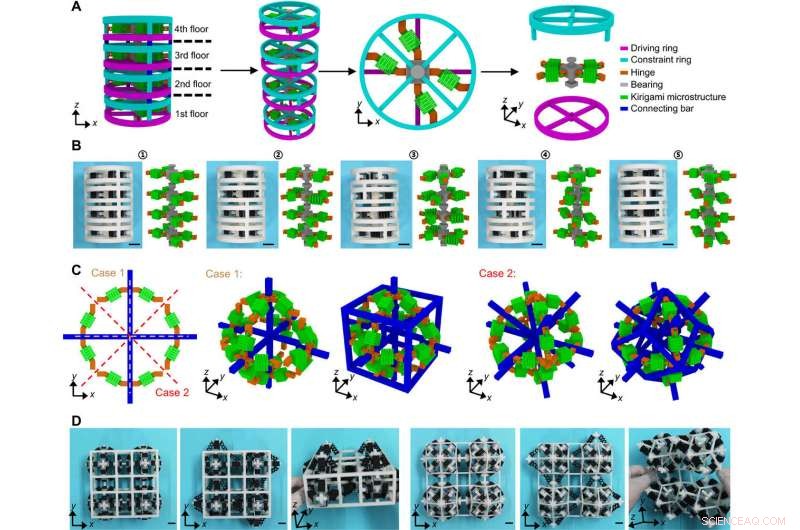
Estrategia de diseño bottom-up y demostración de metamateriales mecánicos multiestables 3D. (A) Ilustración esquemática de un metamaterial mecánico multiestable torsional que consta de cuatro capas direccionables individualmente. Cada capa está compuesta por un anillo de conducción, un anillo restrictivo, bisagras un cojinete, y una estructura de bloques de construcción en forma de X. (B) Imágenes ópticas y resultados FEA de cinco configuraciones estables representativas de un metamaterial mecánico torsional impreso en 3D con los mismos parámetros geométricos que en (A). (C) Ilustración esquemática de los metamateriales mecánicos multiestables cúbicos y octaédricos. Las líneas discontinuas naranjas y rojas indican los ejes de rotación de la celda octagonal para formar metamateriales mecánicos 3D. (D) Demostración experimental de tres configuraciones estables representativas de los metamateriales mecánicos multiestables cúbicos y octaédricos impresos en 3D. Barras de escala, 15 mm. Créditos de las fotos:Hang Zhang, Universidad de Tsinghua. Crédito:Science Advances, doi:10.1126 / sciadv.abf1966
El equipo llevó a cabo un modelado mecánico cuantitativo de las microestructuras kirigami en forma de X basándose en análisis de elementos finitos. Los resultados indicaron un mecanismo de deformación dominado por flexión bajo estiramiento uniaxial con un módulo de tracción y un módulo de compresión mucho más bajos. La energía de deformación calculada indicó tres puntos mínimos para confirmar la inestabilidad de la estructura de bloques de construcción en forma de X. Los científicos también presentaron metamateriales mecánicos multiestables con geometrías cilíndricas 1-D y celosías cúbicas u octaédricas 3D. El diseño permitió dos configuraciones estables adicionales basadas en rotaciones en sentido horario o antihorario, como lo demuestra el perfil de energía. La celda octagonal ofrecía hasta 3 20 configuraciones estables en teoría, que hasta ahora era inaccesible. El número extremo de estados estables proporcionó un concepto prometedor para el procesamiento de información, como se muestra con puertas lógicas ternarias mecánicas y operadores lógicos combinados.

Diseño y demostración experimental de la celda octagonal. Crédito:Science Advances, doi:10.1126 / sciadv.abf1966
Relación entre propiedades mecánicas y diseños geométricos de microestructuras kirigami y estructuras de bloques de construcción en forma de X
A continuación, los científicos buscaron comprender la relación microestructura-propiedad para evaluar el diseño jerárquico de los metamateriales mecánicos multiestables propuestos. Para lograr esto, se centraron en la estructura de bloques de construcción en forma de X y establecieron la conexión de sus parámetros geométricos clave con el paisaje energético resultante. El equipo dividió los parámetros geométricos en dos categorías, una relacionada con la microestructura kirigami y la otra con el compuesto en forma de X. Luego desarrollaron un modelo teórico de deformación finita para predecir la curva de tensión-deformación de la microestructura kirigami, donde los resultados teóricos estaban de acuerdo con los experimentos. El equipo aumentó aún más el módulo de compresión de las microestructuras kirigami al reemplazar la región de conexión con polímeros duros. Las microestructuras simuladas que se deformaron bajo tensión y compresión también coincidieron con las imágenes ópticas.
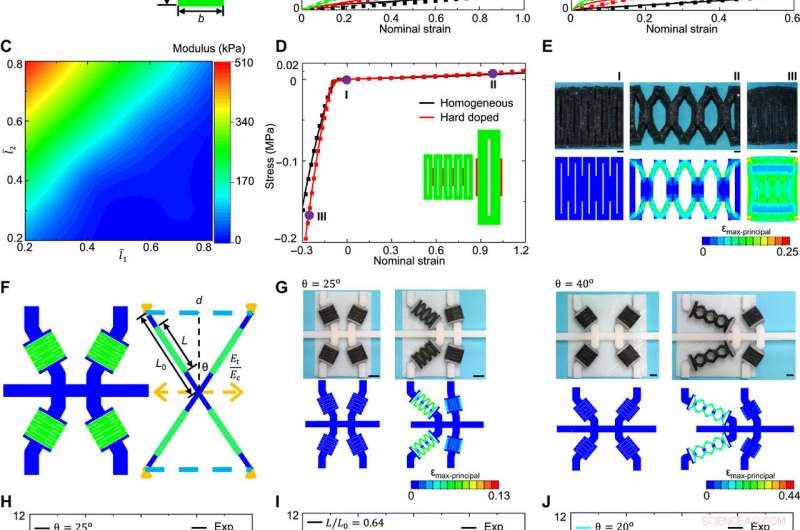
Relación microestructura-propiedad de la estructura de bloques de construcción en forma de X. (A) Ilustración esquemática de la microestructura kirigami y los parámetros clave de diseño. (B) Resultados experimentales y FEA de las curvas de tensión-deformación por tracción de la microestructura kirigami con un rango de diferentes longitudes de corte normalizadas (l¯1 =l1 / ay l¯2 =l2 / a). (C) Gráfico de contorno del módulo de elasticidad efectivo de la microestructura de kirigami con respecto a las longitudes de corte normalizadas (l¯1 y l¯2). (D) Resultados experimentales y FEA de las curvas de tensión-deformación a tracción y compresión de la microestructura kirigami con diseños homogéneos y compuestos. (E) Imágenes ópticas y resultados FEA de la microestructura kirigami compuesta en diferentes estados de carga [marcados en (D)]. (F) Ilustración esquemática de la estructura de bloques de construcción en forma de X. Los parámetros clave de diseño incluyen la relación de módulo (η =Ec / Et) de la microestructura kirigami bajo compresión a la que está bajo tensión, el ángulo θ de la estructura en forma de X, y la relación de longitud (L / L0). (G) Imágenes ópticas y resultados FEA de las dos configuraciones estables de estructuras de bloques de construcción en forma de X con θ =25 ° y 40 ° (izquierda y derecha) para una relación de longitud fija (L / L0 =0,64). (H) Curvas de carga-desplazamiento de la estructura homogénea de bloques de construcción en forma de X con diferentes ángulos (θ), para relación de módulo fija (η =101) y relación de longitud (L / L0 =0,64). (I) Resultados similares en el caso de diferentes relaciones de longitud (L / L0) para una relación de módulo fijo (η =101) y un ángulo (θ =30 °). (J) Curvas de carga-desplazamiento de la estructura compuesta de bloques de construcción en forma de X con diferentes ángulos (θ) para una relación de módulo fija (η =240) y una relación de longitud (L / L0 =0,64). Barras de escala, 1 mm (E) y 5 mm (G). Créditos de las fotos:Hang Zhang, Universidad de Tsinghua Crédito:Science Advances, doi:10.1126 / sciadv.abf1966
Puertas ternarias mecánicas
La flexibilidad de la estructura de bloques de construcción triestable en forma de X permitió aplicaciones de la función lógica ternaria mecánica, que no se podría lograr utilizando bloques de construcción biestables. Por ejemplo, con sistemas mecánicos presentados en trabajos anteriores, Fue muy desafiante combinar muchas puertas básicas para operaciones lógicas complejas. Relativamente, La operación de lógica ternaria podía transmitir una mayor cantidad de información mientras usaba un número reducido de puertas básicas para completar la misma operación y mostró ventajas en la lógica difusa y el procesamiento de señales. El equipo presentó además una puerta NOT ternaria mecánica compuesta por dos módulos que incluyen un convertidor de analógico a digital y un procesador de desplazamiento digital. Se dieron cuenta del convertidor de analógico a digital utilizando la estructura de bloques de construcción triestable en forma de X y desarrollaron el procesador de desplazamiento digital para invertir la dirección del desplazamiento de entrada y realizaron demostraciones experimentales de la funcionalidad de la puerta NOT fabricada.
La operación lógica ternaria de las puertas AND y OR era más complicada en comparación con los operadores binarios. La flexibilidad del diseño modular facilitó operaciones lógicas complejas basadas en las puertas básicas. La gran cantidad de estados estables facilitados con metamateriales mecánicos multiestables permitió operaciones ternarias complejas de múltiples entradas. Por ejemplo, un operador lógico basado en un metamaterial mecánico servía como un convertidor de analógico a digital integrado con un procesador de desplazamiento digital especialmente diseñado para realizar una operación de destino compleja para cuatro entradas diferentes. Los operadores lógicos de esta naturaleza pueden permitir el procesamiento paralelo de entradas en diferentes direcciones para obtener dos salidas independientes.
Aplicaciones en la modulación de amplitud de la vibración de baja frecuencia. (A) Ilustración conceptual del diseño modular del modulador de amplitud. Aquí, el modulador de amplitud trabaja a lo largo de los ejes xey, y el signo de los desplazamientos de entrada / salida es consistente con el signo de los ejes de coordenadas. El módulo 1 sirve para debilitar la transmisión de fuerza, y el módulo 2 combina la fuerza transmitida con las unidades triestables para lograr una salida de desplazamiento regulado. (B) Desplazamientos de entrada y salida a lo largo de la dirección x versus el tiempo para un nivel bajo de amplitud, mostrando la función de filtrar la onda triangular como la onda triangular truncada. Las imágenes ópticas del panel inferior corresponden a los dos estados marcados en las curvas. (C) Resultados similares en el caso de un nivel intermedio de amplitud, mostrando la función de filtrar la onda triangular como onda escalonada. (D) Resultados similares en el caso de un alto nivel de amplitud, mostrando la función de filtrar la onda triangular como onda cuadrada. Barras de escala, 15 mm. Créditos de las fotos:Hang Zhang, Universidad de Tsinghua. Avances científicos, doi:10.1126 / sciadv.abf1966 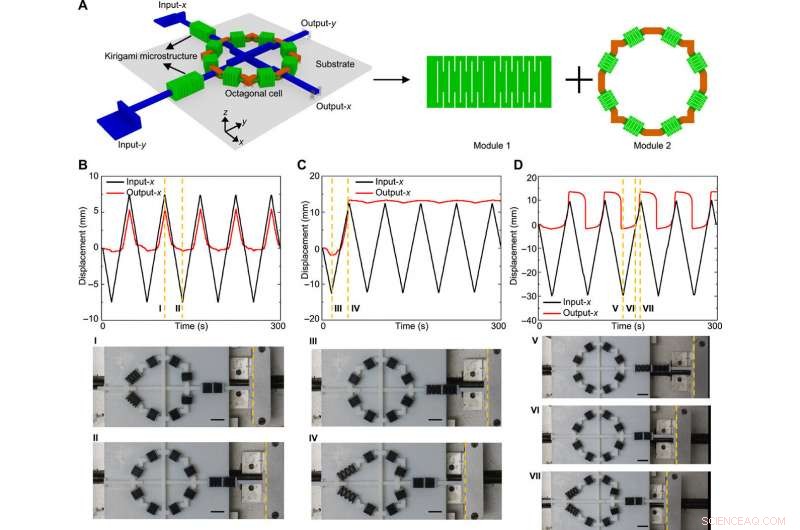
Los científicos presentaron los diseños de un modulador de amplitud bidireccional desarrollado con metamateriales mecánicos multiestables. Filtraron la vibración de baja frecuencia de la configuración experimental, donde el desplazamiento de entrada negativa fue tremendamente suprimido, mientras que el desplazamiento de entrada positivo se transmite con una fidelidad relativamente alta. Dichos dispositivos mecánicos serán efectivos para la integración en robots que trabajen en entornos hostiles como alta radiación y campos magnéticos fuertes. donde los dispositivos electrónicos no funcionarían con la misma eficacia. La capacidad de modular la vibración también se puede utilizar para la supresión de ruido y la comunicación no lineal.

Demostración experimental de los operadores lógicos complejos. Avances científicos, doi:10.1126 / sciadv.abf1966
panorama
De este modo, Hang Zhang y sus colegas detallaron el diseño, Fabricación y caracterización de una clase de metamateriales mecánicos jerárquicos con un número exponencialmente incrementado de estados estables. El equipo comenzó con la estructura de bloques de construcción triestable programable en forma de X y progresó para diseñar metamateriales mecánicos jerárquicos que incluyen geometrías cilíndricas 1-D, Celosías cuadradas 2D y celosías cúbicas u octaédricas 3D. Estos constructos mostraron capacidad para multiestabilidad torsional o multiestabilidad multidireccional controlada independientemente. Los resultados arrojan luz sobre la relación subyacente entre las geometrías microestructurales y el paisaje energético resultante. El equipo mostró aplicaciones en puertas lógicas ternarias mecánicas, incluyendo las tres puertas básicas (Y, NO, y puertas OR) y sus operaciones lógicas combinadas. Los dispositivos mecánicos son prometedores para aplicaciones en robótica blanda y actuadores. Los dispositivos mecánicos serán más ventajosos que los dispositivos eléctricos tradicionales para ahorrar energía y para resistir la corrosión en entornos hostiles.
© 2021 Science X Network