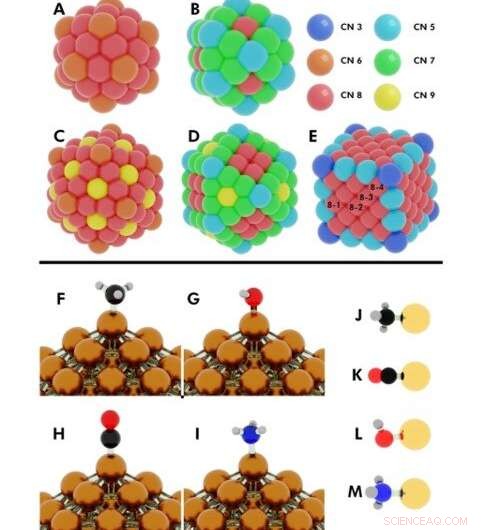
Ilustración de las configuraciones iniciales para varios cálculos de DFT (teoría funcional de densidad) realizados. Superior:Números de coordinación en (A) icosaedro de 55 átomos, (B) cuboctaedro de 55 átomos, (C) icosaedro de 147 átomos, (D) cuboctaedro de 147 átomos, (E) Cubo de 172 átomos. Nanopartículas (NP) donde más de un átomo único comparten el mismo número de coordinación (CN), se denotan con los números 8-1, 8-2, 8-3, 8-4. Crédito:Science Advances, doi:10.1126 / sciadv.aax5101
Las nanopartículas metálicas han recibido una atención sustancial debido a sus aplicaciones en diversos campos de la medicina, catálisis, energía y medio ambiente. Sin embargo, Quedan por comprender las propiedades fundamentales de la adsorción de nanopartículas en una superficie. James Dean y un equipo de investigación interdisciplinario en el departamento de Ingeniería Química, en los EE. UU. introdujo un modelo de adsorción universal para tener en cuenta las características estructurales, composición de metales y diferentes adsorbatos de nanopartículas a través del aprendizaje automático (ML). El modelo se ajusta a una gran cantidad de datos para predecir con precisión las tendencias de adsorción en nanopartículas monometálicas y basadas en aleaciones. La plantilla era simple y proporcionaba datos calculados rápidamente para metales y adsorbatos. El equipo de investigación conectó la adsorción con el comportamiento de estabilidad para avanzar en el diseño de nanopartículas óptimas para aplicaciones de interés. La investigación ahora se publica en Avances de la ciencia .
Las nanopartículas metálicas (NP) tienen aplicaciones importantes en catálisis, que van desde la producción de combustibles y productos químicos, a la energía solar y química. Pero su estabilidad y actividad catalítica generalmente muestran tendencias opuestas, donde los catalizadores muy activos solo pueden operar durante unos pocos ciclos. Una característica clave del grado de funcionalidad catalítica metálica depende de la fuerza de adsorción para una variedad de especies en la superficie del catalizador. Según el principio de Sabatier, desarrollado hace más de un siglo, los catalizadores activos deben unir adsorbatos con una fuerza de unión que no sea ni fuerte ni débil. Si bien las especies fuertemente adsorbidas pueden envenenar la superficie del catalizador, los reactivos débilmente unidos se desorben fácilmente. En un escenario intermedio, los reactivos pueden encontrarse entre sí y reaccionar sobre las superficies catalíticas. Actualmente, los investigadores utilizan métodos de simulación computacional y química teórica para estimular el comportamiento catalítico en catalizadores metálicos con gran precisión para guiar experimentos posteriores en el laboratorio.
Los esfuerzos computacionales se han centrado en seleccionar diferentes catalizadores metálicos para descubrir la energía de enlace "mágica" (BE) de las especies químicas en las superficies de los catalizadores para formar catalizadores muy activos. El diseño in silico de materiales catalíticamente activos, sin embargo, Queda por realizar. Los inconvenientes se deben principalmente a los esfuerzos de diseño que a menudo descuidan la estabilidad de los catalizadores. Los catalizadores NP también poseen un alto grado de heterogeneidad de sitios en su superficie para la adsorción y catálisis. Los científicos habían desarrollado modelos de adsorción para relacionar la energía de enlace de los adsorbatos con las características de la superficie de los NP, como los números de coordinación (CN), para comprender la respuesta de adsorción específica del sitio. Todavía, para mayor claridad, la variación de la energía de enlace (BE) también implica descriptores secundarios como la curvatura y las propiedades electrónicas de los NP.
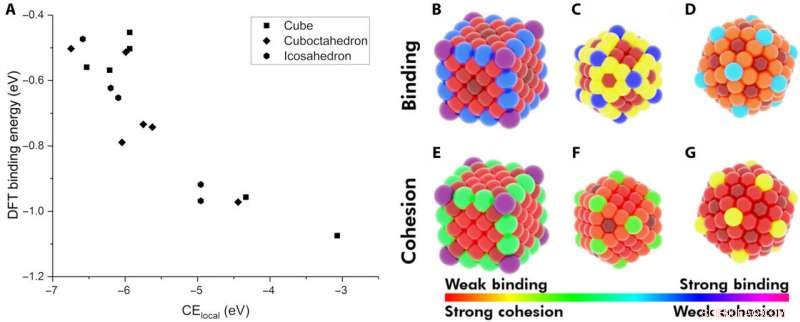
Demostración de la energía cohesiva local (CElocal) como descriptor de la energía de adsorción. (A) El BE del CO en varios sitios de NP de Au en función de CElocal:cubo de 172 átomos (rectángulos), Icosaedro de 147 átomos (hexágonos), y cuboctaedro (rombo) de 147 átomos. Mapa de calor de diferentes sitios en los NP con respecto a su BE de CO (B a D) y a su CElocal (E a G). El esquema de color sigue el rango de unión de CO más fuerte a CElocal más débil (violeta) y de unión más débil a CElocal más fuerte (rojo). Crédito:Science Advances, doi:10.1126 / sciadv.aax5101
En el presente trabajo, Dean y col. Teoría funcional de densidad aplicada (DFT) y técnicas de aprendizaje automático para derivar un modelo simple basado en la física para capturar con precisión la energía de adsorción variable. Estimaron la variable en función del entorno del sitio de adsorción local en la superficie del NP, así como del tipo de NP metálico. El modelo generalizado podría aplicarse a cualquier nanoestructura metálica para comprender el comportamiento de adsorción en el catalizador NP y la estabilidad del catalizador; para cribar y diseñar catalizadores para numerosas aplicaciones.
Los investigadores primero plantearon la hipótesis de los factores más importantes entre los NP monometálicos y los adsorbatos. Luego definieron la energía cohesiva local (CE local ) en metales a granel y CE capturados en NP utilizando un modelo centrado en enlaces, que sumaba cada energía de enlace metal-metal. Aplicando conceptos similares, describieron la estabilidad de los sitios de unión y mostraron cómo los sitios químicamente insaturados (menos enlaces metal-metal) se unían a los adsorbatos con una mayor resistencia. El equipo de investigación se centró en describir la capacidad de unión de un solo par adsorbato-metal. They plotted the DFT-calculated binding energy of carbon monoxide (CO) to a 172-atom gold (Au) cube and a 147-atom gold (Au) cuboctahedron or icosahedron. The team observed a strongly inverse relationship between the local cohesive energy (CE local ) and binding energy (BE) to suggest the strongest adsorption sites to be those exhibiting the weakest local cohesion.
The team further developed their model and performed ordinary least squares (OLS) regression to understand adsorption on monometallic NPs and slabs using three adsorbates [Methyl radical (CH 3 ), CO, hydroxyl radical (OH)] on three different metals (Cu, Ag—silver, Au). The metallic NPs contained different morphologies (172-atom cube, 55- and 147-atom icosahedron and 55- and 147-atom cuboctahedron). They observed that the binding affinity to the adsorbates decreased as the cohesion of the local sites increased. And as the adsorbate's chemical potential increased, they became less stable and bound a metal NP with higher tendency. The direct correlation with the metal Adsorbate (MAD) intuitively described the tendency of the metal to bind the adsorbate.

Parity plot of the model-predicted binding energy (BE) of adsorbates (OH, CO, and CH3) on various metal systems versus the DFT BE (eV). (A) The model both trained and tested on PBE DFT data for NPs (Au/Ag/Cu, 55 to 172 atoms), which includes the nanoparticle cohesive energy (CENP) term. (B) The model both trained and tested on PBE DFT data for NPs (Au/Ag/Cu, 55 to 172 atoms), which does not include the CENP term. (C) The model trained on PBE DFT data for NPs (Au/Ag/Cu, 55 to 172 atoms) and tested against RPBE (revised Perdew-Burke-Ernzerhof model) DFT data for top-site adsorptions on metal surfaces (Au/Ag/Cu). (D) The model both trained and tested on RPBE DFT data for top-site adsorptions on metal surfaces (Au/Ag/Cu) from the slab dataset. Crédito:Science Advances, doi:10.1126/sciadv.aax5101
Dean et al. tested the generalizability of the model and trained the simulation on a single metal or single morphology, although it accurately captured other metals or morphologies as well. The work provided strong evidence that the model captured the underlying physics of the binding interactions, allowing the team to extend the work from non-periodic NPs to periodic slab systems. Computationally inexpensive systems could parameterize the model to extend to larger systems, which was not thus far possible due to the computational costs involved.
Dean et al. then extended the model from monometallic NPs to bimetallic systems. Para estos experimentos, they plotted the BE—trained on monometallic NPs, across several sites of bi-metallic, 55-atom icosahedron NPs (Cu 31 Ag 24 y Cu 22 Ag 33 ). The model very accurately captured trends in adsorption on the bimetallic Cu/Ag NPs as well. This was an interesting result since the scientists had only trained the model on monometallic systems. The results showed the generalizability of the model for both monometallic and bimetallic NPs. Sin embargo, the team will account additional descriptors including binding site electronegativity to understand the adsorption behavior for bimetallic systems in depth.
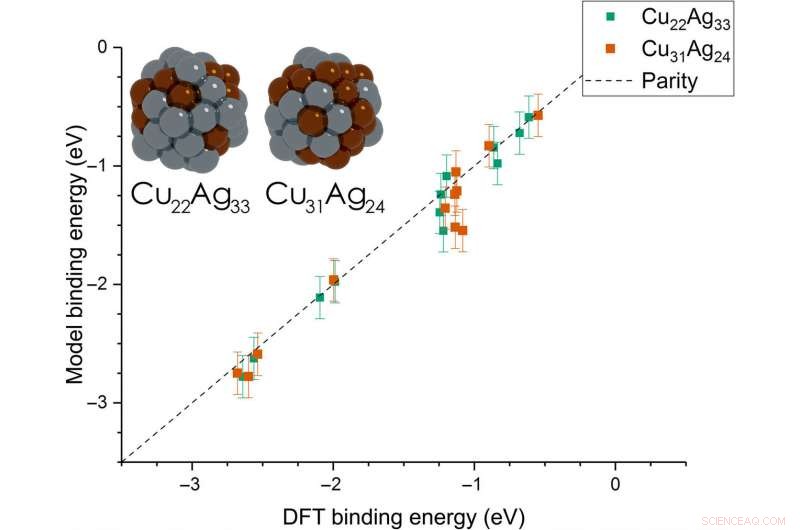
Parity plot between the presently developed model and DFT calculations on icosahedral bimetallic (Cu55−xAgx, x =24, 33) NPs. The model is trained on CH3, CO, and OH adsorbing on monometallic Ag, Cu, and Au NPs and is able to capture adsorption on bimetallic NPs. Images of the two NPs are shown as inset, with copper and silver atoms colored in brown and gray, respectivamente. Crédito:Science Advances, doi:10.1126/sciadv.aax5101
Although Dean et al. trained the ML (machine learning) algorithm to capture the adsorption trends of just one type of d9 metal, it could accurately predict the behavior of similar d9 metals (Cu—coper, Ag and Au). When they trained the model on a dataset of CH 3, CO and OH adsorbed to Cu, Ag and Au NPs, they could also capture general adsorption trends for similar elements in other columns of the periodic table. They then improved the complexity of the machine learning techniques to provide additional avenues to improve the model of adsorption.
De este modo, James Dean and his colleagues developed a simple yet powerful physics-based model to capture trends on the strength of binding interactions between different adsorbates and metal NPs using machine learning techniques. The study was the first to develop an adsorption model that accurately connected the properties of diverse metal NPs with the stability of the adsorption site. The model introduced simple descriptors to capture the adsorption on any site, relative to monometallic and bimetallic NPs. The team generalized the model to effectively stimulate a range of binding interactions, including variations on the types of metals, their composition, sites of adsorption and adsorbates.
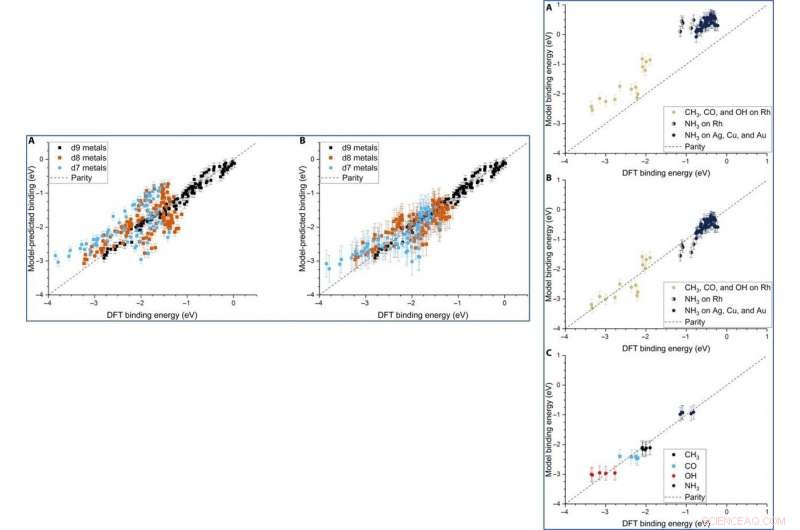
LEFT:The three-descriptor model extended to slab dataset. (A) The model trained on the slab dataset on Cu, Ag, and Au surfaces and tested against the Rh, Ir, Ni, Pd, Pt, Cu, Ag, and Au surfaces from the slab dataset. (B) The equivalent model when trained separately for each column of the d-block, still using the slab dataset. Error bars in every case are the 10-fold cross-validated RMSE of the training set. RIGHT:Extension of the model to Rh and NH3. (A) The model parameterized on our Ag, Cu, and Au NPs adsorbing CH3, CO, and OH and tested against Rh and NH3. (B) The equivalent model with empirical (constant) corrections for Rh and NH3. In the case of NH3 bound to Rh, both corrections are simultaneously applied and indicated by two-colored dots. (C) The model trained on CH3, CO, OH, and NH3 adsorbing on icosahedral/cuboctahedral Rh55. Crédito:Science Advances, doi:10.1126/sciadv.aax5101
Although the team did not test the applicability of the model for ternary systems, the physical properties may remain relevant to accurately model multimetallic systems as well. The adsorption model can accurately describe the binding strength of a variety of molecules on any site of NPs, including alloys. The scientists expect the model to be highly applicable as a screening tool for the high throughput search of potential catalysts.
© 2019 Science X Network