En los últimos años, los físicos han estado tratando de comprender mejor cómo se propaga la información cuántica en sistemas de partículas que interactúan, un fenómeno al que a menudo se hace referencia como "codificación". La lucha en sistemas cerrados, sistemas físicos que sólo pueden intercambiar energía con grados de libertad dentro del sistema, es un rasgo característico de la dinámica cuántica caótica de muchos cuerpos.

En los sistemas abiertos, que pueden intercambiar tanto energía como materia con su entorno, la codificación se ve influenciada por varios factores adicionales, incluidos el ruido y los errores. Si bien los efectos de estas influencias adicionales están bien documentados y conducen, por ejemplo, a la decoherencia, aún no se comprende bien cómo afectan la codificación.

Dos investigadores de la Universidad de California Berkeley (UC Berkeley) y la Universidad de Harvard introdujeron recientemente un nuevo marco, publicado en Physical Review Letters. , que proporciona una imagen universal de cómo se produce la codificación de información en sistemas cuánticos abiertos. Su marco ofrece un punto de vista particularmente simple sobre cómo comprender y modelar la propagación de errores en un sistema cuántico abierto y podría ayudar a explicar algunas observaciones previamente desconcertantes recopiladas en experimentos de resonancia magnética.

"Norm y yo hemos trabajado juntos en varios proyectos centrados en la codificación de información cuántica", dijo a Phys.org Thomas Schuster, uno de los investigadores que llevó a cabo el estudio.

"Algunos de nuestros trabajos se centraron en cómo medir la codificación y otros en para qué podría ser útil la codificación. En todos estos proyectos, seguía surgiendo una pregunta natural:¿Cómo se modifica la codificación mediante errores (es decir, 'sistema abierto'? dinámica) que inevitablemente ocurren en experimentos de la vida real. Aunque esta pregunta era claramente importante, no teníamos ningún marco satisfactorio para responderla."

Mientras exploraban esta cuestión, Schuster y Yao se dieron cuenta de que podría resultar útil considerar las cosas desde una perspectiva experimental. Esto finalmente condujo a su reciente estudio.

"En la dinámica de sistemas abiertos, los errores perturban el sistema y nos gustaría saber la sensibilidad de nuestro experimento a estas perturbaciones", dijo Schuster. "Esto sugiere que la sensibilidad de un experimento a los errores debe estar relacionada con cómo se codifica la información. Partiendo de esta idea inicial, trabajamos para hacer precisa la conexión entre los errores y la codificación, y para analizar sus consecuencias para los sistemas físicos y los experimentos de interés. "

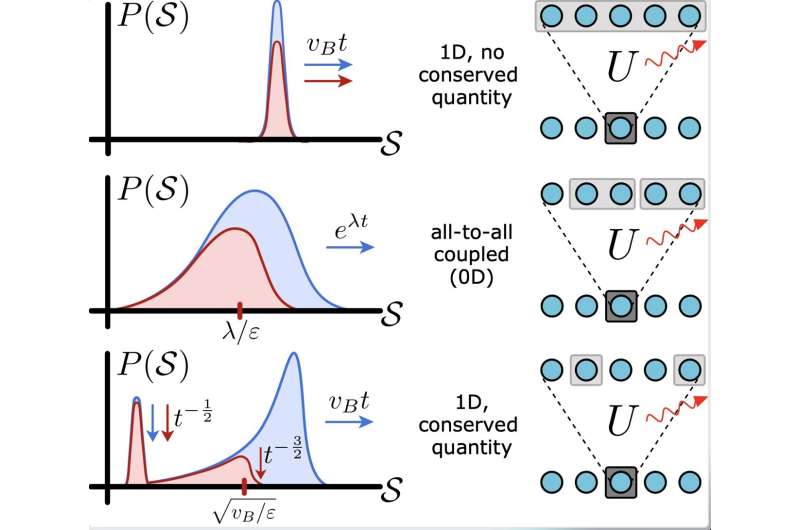
La idea clave detrás del reciente estudio de Schuster y Yao es que la codificación de información en un sistema abierto es en cierto modo independiente de la naturaleza microscópica de los errores mismos. Más bien, todo depende de cómo estos errores afectan las llamadas "distribuciones del tamaño del operador", una caracterización de la complejidad del operador en función de la evolución temporal.

"La dinámica de la distribución del tamaño de los operadores determina de forma precisa cómo se propagan los errores", explicó Schuster. "En su nivel más simple, esto toma la forma de dos ecuaciones diferenciales acopladas. La entrada a las ecuaciones es cómo cambia la distribución del tamaño de los operadores, mientras que la salida puede considerarse como una predicción precisa de cómo se propagan los errores".

Si bien algunos estudios anteriores habían insinuado esta conexión, hasta ahora nadie la había formulado de manera clara y precisa. Al hacerlo, Schuster y Yao descubrieron que la interacción entre errores y codificación tenía muchos más matices de lo que se había previsto anteriormente.

"Otro resultado novedoso de nuestro trabajo es que los errores también modifican el comportamiento de la información que se codifica", dijo Schuster. "Esto conduce a una interesante interacción entre errores y codificación, descrita por las ecuaciones mencionadas anteriormente. El resultado de esta interacción depende de la naturaleza de la dinámica misma y puede usarse como una caracterización intrínseca de esta dinámica, además de predecir varias propiedades. de experimentos."

Un entorno particularmente fructífero para aplicar el marco de Schuster y Yao surge en ciertos experimentos que involucran la llamada dinámica "ergódica" de muchos cuerpos. Esto podría realizarse y validarse en futuros trabajos.

"Una agradable sorpresa que descubrimos mientras estábamos completando nuestros resultados es que nuestro marco también se aplica a una gran clase de experimentos, llamados 'eco de Loschmidt', que han sido de interés para las comunidades de resonancia magnética nuclear (RMN) y caos cuántico. durante varias décadas", afirmó Schuster. "El eco de Loschmidt es un experimento mental de larga data en termodinámica, que se remonta a Josef Loschmidt y la fundación de la termodinámica en el siglo XIX."

Si bien los métodos experimentales en torno al eco de Loschmidt han seguido mejorando, tanto en experimentos de simulación cuántica como en estudios de resonancia magnética de estado sólido, la interpretación de estas señales, especialmente para los hamiltonianos que interactúan en este último contexto, ha seguido siendo un desafío.

"Los experimentalistas adaptaban varias formas funcionales (por ejemplo, gaussianas, exponenciales o sigmoideas) a sus datos, pero nunca tuvieron una explicación de por qué un experimento específico siguió una forma funcional en lugar de otra", dijo Schuster. "A principios de la década de 2000, los investigadores descubrieron un marco para describir el eco de Loschmidt en sistemas cuánticos de pocos cuerpos; sin embargo, el caso de los sistemas de muchos cuerpos sigue siendo una cuestión abierta. Creemos que nuestro marco puede proporcionar una respuesta a esto. pregunta."

Además de arrojar luz sobre cómo se propagan los errores en sistemas cuánticos abiertos de muchos cuerpos, el trabajo reciente también sugiere que los datos de los experimentos de eco de Loschmidt podrían contener más información de la que parece originalmente.

"La interacción de los errores y la dinámica de distribución del tamaño del operador determina la forma funcional del eco de Loschmidt", dijo Schuster. "Confiamos en que este sea el caso en los modelos de juguetes que podemos estudiar numéricamente y, en trabajos futuros, esperamos proporcionar un análisis más detallado de los datos experimentales del eco de Loschmidt para confirmar que nuestro marco también se aplica allí. Hay varios hay indicios que sugieren fuertemente que sí, lo cual me parece bastante emocionante."

De cara al futuro, Schuster y Yao están interesados ​​en aplicar su nuevo marco a una variedad de otros experimentos. También planean explorar las implicaciones de sus resultados para la simulación clásica de sistemas cuánticos abiertos.

"Nos preguntamos si nuestra comprensión de la difusión de información en estos sistemas abiertos puede realmente proporcionar información sobre cuánta ventaja cuántica se puede aprovechar de ellos", dice Yao. "Y por otro lado, si se pueden diseñar nuevos algoritmos para simular eficientemente sistemas cuánticos abiertos".

Más información: Thomas Schuster et al, Crecimiento de operadores en sistemas cuánticos abiertos, Cartas de revisión física (2023). DOI:10.1103/PhysRevLett.131.160402

Información de la revista: Cartas de revisión física

© 2023 Red Ciencia X