Las redes pueden representar sistemas cambiantes, como la propagación de una epidemia o el crecimiento de grupos en una población de personas. Pero la estructura de estas redes también puede cambiar a medida que los vínculos aparecen o desaparecen con el tiempo. Para comprender mejor estos cambios, los investigadores suelen estudiar una serie de "instantáneas" estáticas que capturan la estructura de la red durante un breve periodo de tiempo.
Los teóricos de las redes han buscado formas de combinar estas instantáneas. En un nuevo artículo en Physical Review Letters , un trío de investigadores afiliados a SFI describen una forma novedosa de agregar instantáneas estáticas en grupos más pequeños de redes y al mismo tiempo preservar la naturaleza dinámica del sistema. Su método, inspirado en una idea de la mecánica cuántica, implica probar pares sucesivos de instantáneas de redes para encontrar aquellas cuya combinación daría como resultado el menor efecto en la dinámica del sistema, y luego combinarlas.
Es importante destacar que puede determinar cómo simplificar el historial de la estructura de la red tanto como sea posible manteniendo la precisión. Las matemáticas detrás del método son bastante simples, dice la autora principal Andrea Allen, ahora científica de datos en el Hospital Infantil de Filadelfia.
"Estamos muy entusiasmados de poder compartirlo y es sorprendente que nadie más haya publicado esta idea exacta en la última década", dice Allen. Colaboró con el profesor Cris Moore, físico y matemático del SFI, y con Laurent Hébert-Dufresne, científico de la complejidad de la Universidad de Vermont y ex becario de la Fundación James S. McDonnell del SFI.
En el artículo publicado, el método no parece complicado; en realidad, evolucionó a lo largo de años tanto dentro como fuera de SFI. La colaboración comenzó en 2015 cuando Allen, entonces estudiante de matemáticas, visitó SFI durante un mes en el invierno y luego, en el verano de 2016, regresó para participar en el programa de Experiencias de investigación para estudiantes universitarios (ahora llamado programa de Investigación de Complejidad de Pregrado). .
Hébert-Dufresne había obtenido un gran conjunto de datos, adquirido a partir de datos de teléfonos satelitales, que utilizaba "pings" de teléfonos móviles para mostrar cómo se movía la gente. Estaba interesado en encontrar comunidades, pero también quería poder medir si diferentes comunidades requerían una resolución de datos diferente.
"Por ejemplo, ¿deberían los sistemas de vigilancia epidémica ser uniformes en todas las comunidades cuando sabemos que diferentes comunidades tienen comportamientos diferentes?"
Esa pregunta llevó a más preguntas:"¿A qué nivel podemos agregar esto manteniendo las diferencias? ¿Y cómo lo sabemos?". pregunta Allen. "No queremos perder la integridad de la red que intentamos estudiar".
Trajeron a Moore para que intercambiara ideas sobre cómo saber qué diferencias eran importantes para la estructura general y cuáles eran menos importantes. Luego, después de un tiempo, archivaron el proyecto.
Allen dejó la academia para convertirse en desarrollador de software y Hébert-Dufresne inició su propio grupo de investigación en Vermont. Pero sería una breve pausa. Dos años más tarde, Allen se unió al grupo de Hébert-Dufresne en Vermont como estudiante de posgrado y continuaron donde lo habían dejado.
"Siempre dijimos:'terminemos con esto ahora'", dice Allen. "Esto se convirtió en una especie de broma durante ocho años".
En el último esfuerzo, los investigadores identificaron una forma sencilla de aproximar el error y utilizarlo en combinaciones sucesivas de pares de redes. En el artículo, los investigadores utilizan la propagación de enfermedades como vara de medir para evaluar y validar el método.
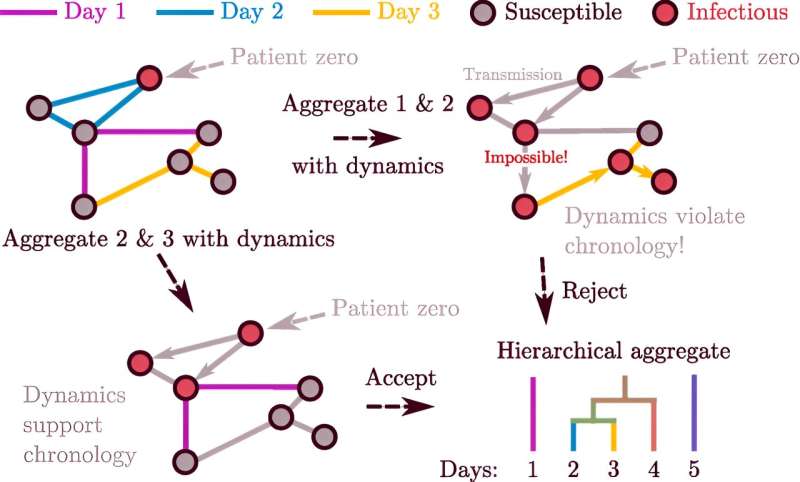
"Supongamos que hay una pandemia", dice Moore. Si dos personas (Alice y Bob) se juntan, y luego otras dos personas (por ejemplo, Bob y Charlene) se juntan, entonces la enfermedad podría propagarse de Alice a Charlene, pero no al revés. El orden de estos enlaces es importante, lo que significa que es engañoso combinarlos en una sola instantánea (y tratarlos como si fueran simultáneos).
El nuevo método toma prestada una idea de la mecánica cuántica para identificar este tipo de errores. En ese campo, el "conmutador" puede revelar cuánto importa el orden en los cálculos que involucran cosas como la energía y el impulso. En la nueva aplicación, los investigadores utilizaron un conmutador para decidir cuánto importa el orden y cuándo es preciso combinar instantáneas.
"Esto nos permite simplificar el historial de la estructura de la red tanto como sea posible manteniendo la precisión", dice Moore. También apunta a una manera de domesticar un conjunto de datos enorme y difícil de manejar y convertirlo en un conjunto de redes más pequeño y manejable.
Allen dice que podría extenderse a otros sistemas dinámicos, como la difusión de información a través de una red social.
Más información: Andrea J. Allen et al, Compresión de la cronología de una red temporal con conmutadores de gráficos, Cartas de revisión física (2024). DOI:10.1103/PhysRevLett.132.077402
Proporcionado por Instituto Santa Fe