Los físicos utilizan modelos teóricos para estudiar cantidades físicas, como la masa de los núcleos, cuando no cuentan con datos experimentales. Sin embargo, utilizar un único modelo teórico imperfecto puede conducir a resultados engañosos. Para mejorar la calidad de las predicciones extrapoladas, los científicos pueden utilizar varios modelos diferentes y mezclar sus resultados. De esta manera, los científicos aprovechan al máximo la sabiduría colectiva de múltiples modelos y obtienen la mejor predicción a partir de la información experimental más actual.

Para mejorar la previsibilidad de modelos computacionales complejos, un equipo de físicos y estadísticos nucleares propuso un método estadístico novedoso. Este método utiliza un proceso estadístico llamado teorema de Bayes para revisar la probabilidad de una hipótesis a medida que se obtienen nuevos datos. El trabajo está publicado en la revista Scientific Reports .

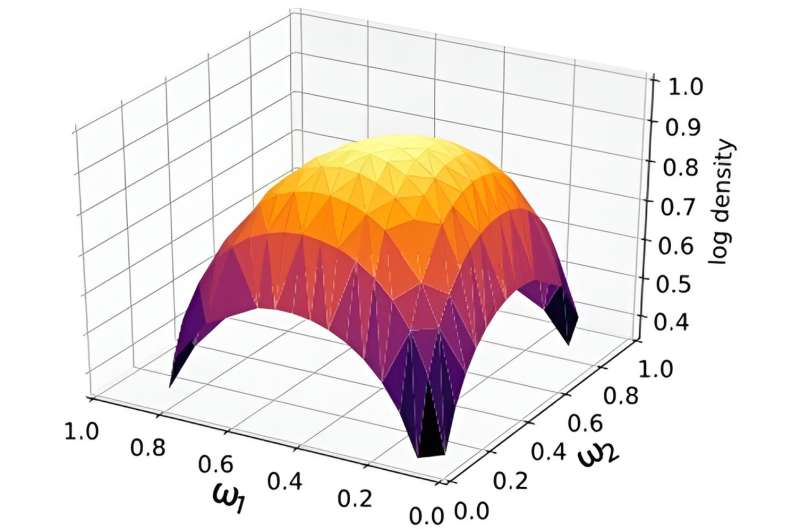
El marco de aprendizaje automático resultante utiliza la llamada distribución Dirichlet. Este proceso estadístico combina los resultados de varios modelos imperfectos. Los investigadores demostraron la capacidad de las técnicas de mezcla propuestas para extraer datos sobre masas nucleares.

Esta investigación demostró que las combinaciones de modelos globales y locales tienen un rendimiento excelente tanto en la precisión de sus predicciones como en la cuantificación de la incertidumbre. Estas mezclas parecen ser preferibles al modelo bayesiano clásico de promedio, el enfoque convencional. Además, el análisis de los investigadores indica que mejorar las predicciones de los modelos mediante una combinación directa conduce a extrapolaciones más sólidas que la combinación de modelos corregidos.