
Los investigadores de ETH han logrado atrapar iones mediante campos eléctricos y magnéticos estáticos y realizar operaciones cuánticas con ellos. En el futuro, estas trampas podrían utilizarse para crear ordenadores cuánticos con muchos más bits cuánticos de los que han sido posibles hasta ahora.
Los estados energéticos de los electrones en un átomo siguen las leyes de la mecánica cuántica:no están distribuidos continuamente sino restringidos a ciertos valores bien definidos; esto también se llama cuantificación. Estos estados cuantificados son la base de los bits cuánticos (qubits), con los que los científicos quieren construir ordenadores cuánticos extremadamente potentes. Para ello, los átomos deben enfriarse y quedar atrapados en un solo lugar.
Se puede lograr una fuerte captura ionizando los átomos, lo que significa darles una carga eléctrica. Sin embargo, una ley fundamental del electromagnetismo establece que los campos eléctricos constantes en el tiempo no pueden atrapar una sola partícula cargada. Por otro lado, añadiendo un campo electromagnético oscilante se obtiene una trampa de iones estable, también conocida como trampa de Paul.
De este modo, en los últimos años ha sido posible construir ordenadores cuánticos con trampas de iones que contienen alrededor de 30 qubits. Sin embargo, con esta técnica no es posible crear ordenadores cuánticos mucho más grandes. Los campos oscilantes dificultan la combinación de varias de estas trampas en un solo chip, y su uso calienta la trampa, un problema más importante a medida que los sistemas crecen. Mientras tanto, el transporte de iones se limita a pasar a lo largo de secciones lineales conectadas por cruces.
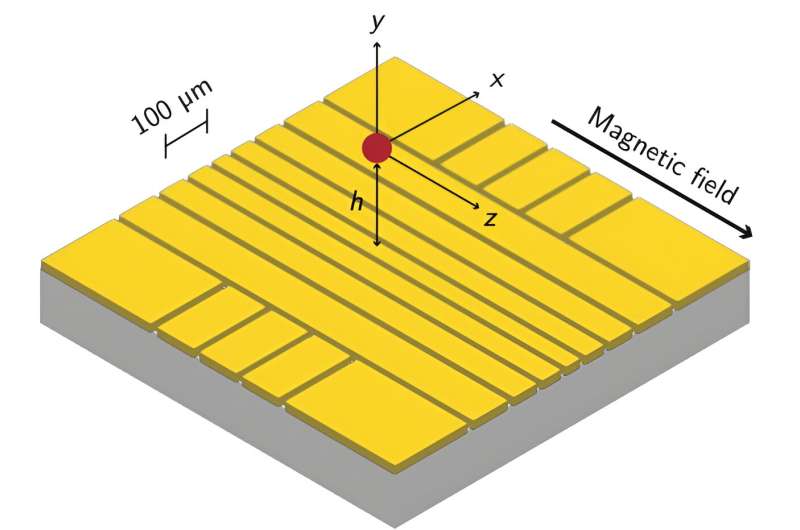
Trampa de iones con campo magnético
Un equipo de investigadores de ETH Zurich dirigido por Jonathan Home ha demostrado que también se pueden construir trampas de iones adecuadas para su uso en computadoras cuánticas utilizando campos magnéticos estáticos en lugar de campos oscilantes. En aquellas trampas estáticas con un campo magnético adicional, llamadas trampas de Penning, se realizaban tanto el transporte arbitrario como las operaciones necesarias para los futuros superordenadores. Los investigadores publicaron recientemente sus resultados en la revista científica Nature. .
"Tradicionalmente, las trampas Penning se utilizan cuando se quiere atrapar muchos iones para experimentos de precisión, pero sin tener que controlarlos individualmente", dice Ph.D. estudiante Shreyans Jain. "En cambio, en los ordenadores cuánticos más pequeños, basados en iones, se utilizan trampas de Paul."
La idea de los investigadores de ETH de construir futuros ordenadores cuánticos utilizando también trampas de Penning suscitó inicialmente escepticismo por parte de sus colegas por diversas razones. Las trampas Penning requieren imanes extremadamente fuertes, que son muy caros y bastante voluminosos.
Además, todas las realizaciones anteriores de las trampas de Penning habían sido muy simétricas, algo que violan las estructuras a escala de chip utilizadas en ETH. Colocar el experimento dentro de un imán grande dificulta guiar los rayos láser necesarios para controlar los qubits hacia la trampa, mientras que los fuertes campos magnéticos aumentan el espacio entre los estados de energía de los qubits. Esto, a su vez, hace que los sistemas láser de control sean mucho más complejos:en lugar de un simple láser de diodo, se necesitan varios láseres sincronizados en fase.

Transporte en direcciones arbitrarias
Sin embargo, Home y sus colaboradores no se dejaron disuadir por esas dificultades y construyeron una trampa Penning basada en un imán superconductor y un chip microfabricado con varios electrodos, que se produjo en el Physikalisch-Technische Bundesanstalt en Braunschweig. El imán utilizado genera un campo de 3 Tesla, casi 100.000 veces más fuerte que el campo magnético de la Tierra. Utilizando un sistema de espejos enfriados criogénicamente, los investigadores de Zurich lograron canalizar la luz láser necesaria a través del imán hacia los iones.
Los esfuerzos dieron sus frutos:un único ion atrapado, que puede permanecer en la trampa durante varios días, ahora se puede mover arbitrariamente en el chip, conectando puntos "en línea recta" mediante el control de los diferentes electrodos; esto antes no era posible con el antiguo enfoque basado en campos oscilantes. Dado que no se necesitan campos oscilantes para atrapar, muchas de esas trampas se pueden empaquetar en un solo chip.
"Una vez cargados, podemos incluso aislar completamente los electrodos del mundo exterior y así investigar con qué intensidad las influencias externas perturban los iones", afirma Tobias Sägesser, que participó en el experimento como doctor. estudiante.
Los investigadores también demostraron que los estados de energía del qubit del ion atrapado también podrían controlarse manteniendo las superposiciones de la mecánica cuántica. El control coherente funcionó tanto con los estados electrónicos (internos) del ion como con los estados de oscilación cuantificados (externos), así como para acoplar los estados cuánticos internos y externos. Este último es un requisito previo para crear estados entrelazados, que son importantes para las computadoras cuánticas.
Como siguiente paso, Home quiere atrapar dos iones en trampas de Penning vecinas en el mismo chip y demostrar así que también se pueden realizar operaciones cuánticas con varios qubits. Esta sería la prueba definitiva de que es posible realizar ordenadores cuánticos utilizando iones en trampas de Penning. El profesor también tiene otras aplicaciones en mente. Por ejemplo, dado que los iones de la nueva trampa se pueden mover con flexibilidad, se pueden utilizar para sondear campos eléctricos, magnéticos o de microondas cerca de superficies. Esto abre la posibilidad de utilizar estos sistemas como sensores atómicos de propiedades de superficies.
Más información: Shreyans Jain et al, Microtrampa Penning para computación cuántica, Naturaleza (2024). DOI:10.1038/s41586-024-07111-x
Proporcionado por ETH Zurich