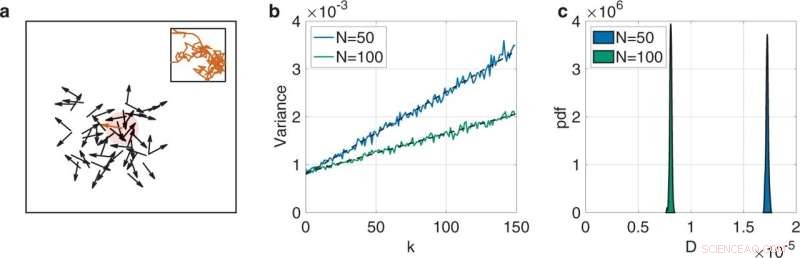
Ilustración del enfoque propuesto para inferir el tamaño de un conjunto de partículas de Vicsek autopropulsadas a partir del movimiento de una sola unidad. Realizamos 1000 repeticiones en las que registramos el rumbo de una partícula en el colectivo para diferentes valores de la longitud del lado L del dominio cuadrado, la velocidad s, el número de partículas N y el ruido η. a Esquema de un experimento numérico para N = 20, donde mostramos una instantánea temporal del sistema (la partícula focal está en rojo y su círculo de interacción está sombreado). El recuadro muestra una trayectoria de muestra de la partícula focal que evoluciona desde la instantánea durante 150 pasos de tiempo. b Varianza Yk del rumbo de la partícula focal en función del tiempo k para dos tamaños de sistema cuando η = 0.1, s = 3 y L = 4, con las líneas negras discontinuas que marcan el ajuste lineal. Duplicar el tamaño reduce a la mitad el coeficiente de difusión (N = 50: D = 1.67 × 10 −5 , y N = 100: D = 8.41 × 10 −6 ). c Distribución del coeficiente de difusión tal como se estimaría a partir de observaciones de diferentes partículas focales en el colectivo. Crédito:Física de las comunicaciones (2022). DOI:10.1038/s42005-022-00864-9
Las dinámicas colectivas son omnipresentes en el mundo natural. Desde circuitos neuronales hasta grupos de animales, hay innumerables casos en los que las interacciones entre un gran número de unidades elementales otorgan patrones sorprendentemente complejos de belleza tentadora al colectivo. Uno de los objetivos de larga data de los investigadores en muchos campos es comprender los comportamientos de un gran grupo de unidades individuales mediante el seguimiento de las acciones de una sola unidad. Por ejemplo, un ornitólogo puede aprender muchas cosas sobre el comportamiento de una bandada al monitorear solo un ave.
De mayor dificultad es comprender el tamaño de una colección de unidades al observar una sola unidad. No importa cuántas aves se marquen con el equipo de monitoreo, nunca se puede estar seguro de haber marcado toda la parvada. Sin embargo, aunque la capacidad de calcular el tamaño de un colectivo a partir de los comportamientos individuales sería una herramienta clave para cualquier campo, solo hay un puñado de artículos recientes que intentan abordar el problema aparentemente irresoluble.
En un estudio recientemente publicado que aparece en Communications Physics , investigadores dirigidos por Maurizio Porfiri, profesor del Instituto de Ingeniería Mecánica y Aeroespacial e Ingeniería Biomédica, y miembro del Centro para la Ciencia y el Progreso Urbano (CUSP) de la Escuela de Ingeniería NYU Tandon; y Pietro De Lellis de la Universidad de Nápoles, Italia, ofrecen un paradigma para resolver este problema, que se basa en preceptos que se remontan al trabajo de Einstein.
Al observar un sistema de partículas de Vicsek autopropulsadas, una conceptualización matemática del movimiento y el enjambre de partículas, como modelo universal para la dinámica colectiva, muestran que la tasa de crecimiento en el tiempo del rumbo cuadrático medio de cualquier partícula es suficiente para predecir el número de partículas en el sistema bajo parámetros particulares, como una temperatura conocida y constante.
En términos generales, el estudio proporciona un método riguroso respaldado matemáticamente para inferir el tamaño de un colectivo realista a partir de las mediciones de algunas de sus unidades, cuyo movimiento aleatorio contiene las huellas de todo el sistema. Los fundamentos teóricos del método proporcionan más evidencia de las analogías identificadas por Einstein entre la investigación interdisciplinaria en el comportamiento colectivo de los grupos de animales y la física moderna. El trabajo futuro en este sentido puede estudiar colectivos reales, desde enjambres de insectos hasta bandadas de pájaros, cardúmenes de peces y multitudes humanas. Un gran avance en la estimación del tamaño de una red (en su mayoría oculta)